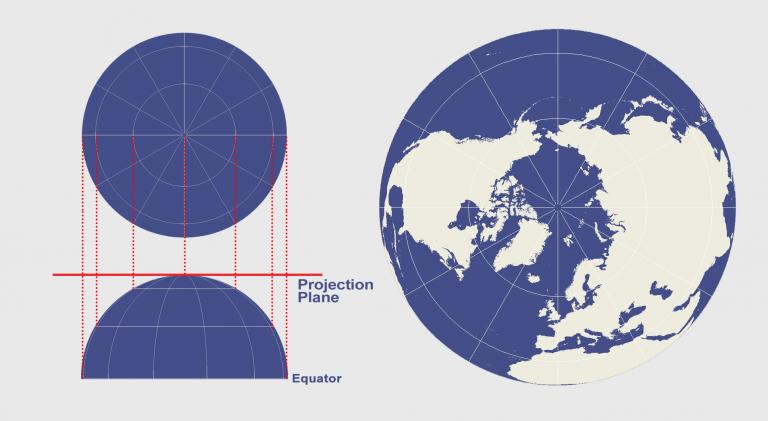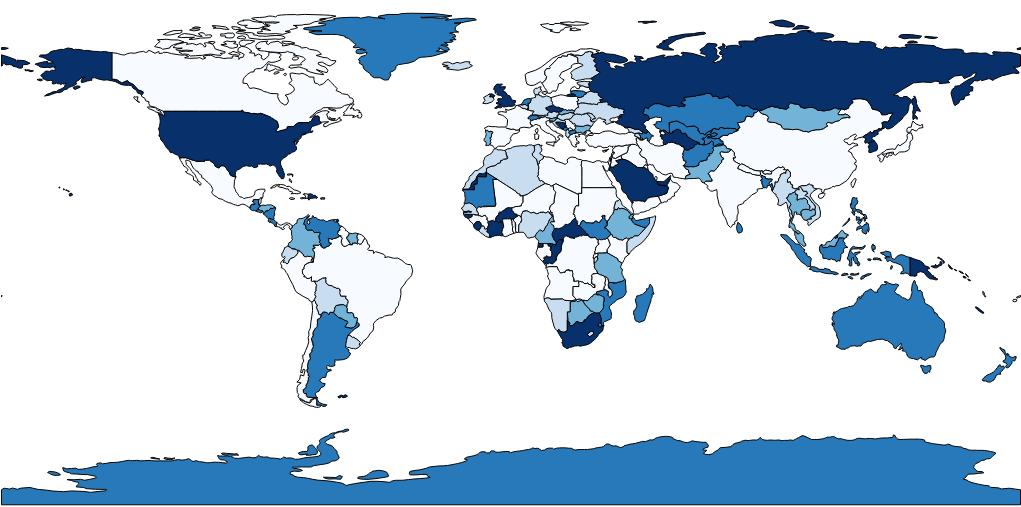
什么是 Choropleth 地图?
等值线图根据定量数据使用不同的阴影和颜色。
但是等值线图的问题是:有太多方法可以对数据进行分类。
但是他们每个人之间有什么区别呢?
今天,您将在我们的数据分类指南中学习如何选择最好的方法对等值线图中的数据进行分类。
选择您的课程数量
首先,您必须聚合基于多个类的数据。当你有更多的类时,你会得到更多的变化,有时会使分离阴影变得更加困难。如果您想测试不同的阴影, ColorBrewer有一个颜色建议工具。
例如,这里有10 个类:

虽然更少的类在类之间提供更少的分离,例如下面的5 个类。

毕竟,您决定的类别数量实际上取决于地图的用途。
选择您的数据分类方法
其次,您必须决定如何对数据进行分类。换句话说,数据分类使用边界将您的数据排列成不同的类。您可以使用等间隔模式分隔您的班级:

或者,您可以选择一种分位数类型的分类器,它以不同的方式排列数据(更多内容见下文)
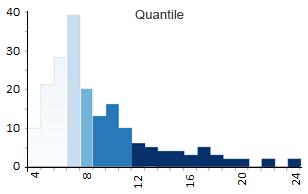
每种数据分类技术都会产生独特的等值线图。但它们都向地图阅读器描绘了一个不同的故事。您必须意识到的一件事是,您在每个等值线图中使用相同的数据,但真正改变的是您对数据进行分类的方式。
您想有效地传达数据吗?查看10 项数据可视化认证和课程的列表。
创建等值线图
您必须意识到的最重要的事情是,对于我们创建的每一个等值线图,我们都使用相同的数据。发生变化的是我们对数据进行分类的方式。
在此示例中,我们计算国家/地区名称中的字母数。例如:
- 马里、古巴、秘鲁等是四个字母的国家。
- 而波斯尼亚和黑塞哥维那有 22 个字符。
如果你绘制出4到22个字符,它会有很多颜色。
例如,四个字母的国家/地区是最浅的绿色阴影。随着字母数的增加,阴影变暗。
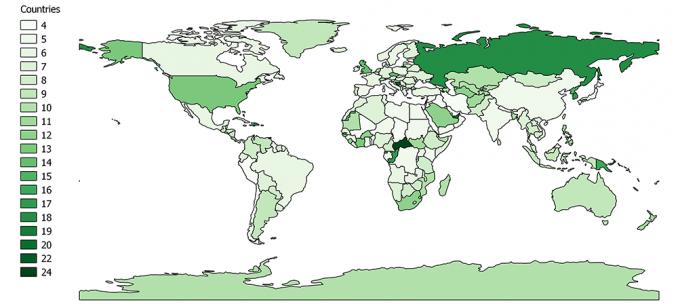
标题 – 按国家/地区字符数绘制的 Choropleth 地图阴影
哪个国家属于哪个组?很难说。
所以这就是我们使用数据分类的原因。当我们按类别分组时,阴影较少,我们按组聚合数据。
最终,问题是我们如何定义这些类边界或容器?换句话说,我们如何对数据进行分组?
首先,让我们尝试将类分成均匀间隔的组,如下面的等间隔,看看会发生什么。
等区间数据分类
等间隔分级即切即干。它所做的只是将班级分成相等的组。

- 第 1 类:4 – 8(113 个国家有四个、五个、六个、七个或八个字母)
- 2 级:8 – 12 (41)
- 3 级:12 – 16 (12)
- 4 级:16 – 20 (8)
- 5 级:20 – 24 (2)
一个国家的最小字符数是 4,例如秘鲁。最大字符数为 24 ,即中非共和国。当您在地图上绘制每个国家及其字符数时,它看起来像这样(括号表示计数):
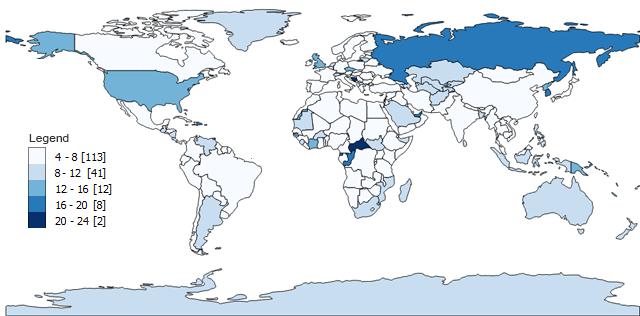
等区间数据分类用最小值减去最大值( 24-4=20 )。在我们的示例中,我们生成了 5 个类,但类的数量完全由您决定。然后,它将 20 除以 5,得到一个区间 ( 20/5=4 )。
几乎总是,等间隔等值线图会导致每个类别的国家数量不相等。例如,第 1 类有 176 个国家中的113 个国家有四个、五个、六个和七个字母。
但是,只有 2 个国家的字母超过 20 个。因此,与只有 2 个深色阴影相比,这张地图显示了更多的浅色阴影。
但是,如果您希望每个类别中的国家/地区数量接近相等,会发生什么情况?那是你应该使用分位数图的时候。
分位数(等计数)分类
分位数图尝试对 5 个类中的每个类中相同数量的要素进行分箱。换句话说,分位数图试图排列组,使它们具有相同的数量。因此,阴影在分位数类型的地图中看起来分布均匀。

- 第 1 类:4 – 6(56 个国家有 4、5 或 6 个字母的名称)
- 2 级:6 – 7 (38)
- 第 3 班:7 – 8 (19)
- 4 级:9 – 11 (36)
- 5 级:12 – 24 (27)
分位数图采用特征数量(在我们的例子中是 176 个国家)。然后,它将总数除以类数以获得平均值 ( 176/5=35.2 )。最后,分位数图计算每组中的数量,并尽可能接近平均值排列。
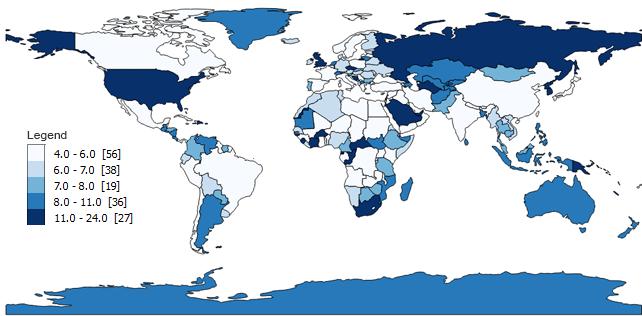
您可以看到每个类的计数看起来非常相似并且接近 35.2 。对于每一类,计数都不会太多或太少。
尽管分位数等值线图采用平衡风格,但它们也可能具有误导性。它们具有误导性,因为人们倾向于查看其中一种色调并将其归入同一类别。例如,一个 12 个字母的国家/地区与一个 24 个字母的国家/地区具有相同的深色阴影……这其中的正义在哪里?
自然休息 (Jenks) 分类
关于 Natural Breaks (Jenks) 分类,首先要记住的是它是等值线图的优化方法。简而言之,它会安排每个分组,因此每个类别或阴影的变化较小。
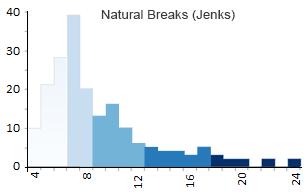
- 1 级:4 – 6 (56)
- 2 级:6 – 8 (57)
- 3 级:8 – 12 (41)
- 4 级:12 – 18 (18)
- 5 级:18 – 24 (4)
Natural Breaks (Jenks) 采用迭代方法,将类之间的偏差平方和与数组均值进行比较。然后,该算法使用方差拟合优度,其中 1 为完美拟合,0 为差拟合。
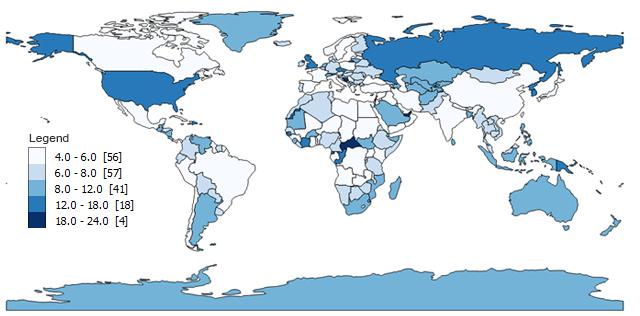
Natural Breaks 数据分类方法的创始人是一位名叫 George Frederick Jenks 的制图师。他专门研究人们在看地图时的眼球运动。这张地图的结果看起来也很棒。
您可以看到这种数据分类方法如何最大限度地减少每个组中的差异。由于我们有很多较短的国家/地区名称,它会找到合适的类别范围。但它仍然设法将具有较长国家/地区名称的异常值归为一类。
标准偏差分类
标准偏差是一种统计技术类型的地图,基于数据与平均值的差异程度。您测量数据的均值和标准差。然后,每个标准偏差都会成为您的等值线图中的一个类。
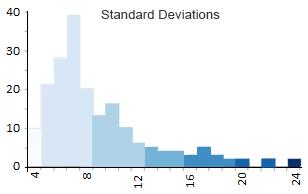
在我们的例子中,平均字符数约为 8.5,标准差为 3.7 个字符。因此,所有具有 5 到 8 个字符的国家/地区将被置于 0 到 -1 标准差分组中。同样,具有 9 到 12 个字母的国家/地区在 0 到 1 个标准偏差范围内分组,如下所示:

- 1 级:<-1 σ (9)
- 2 级:-1 至 0 σ (104)
- 3 级:0 至 1 σ (41)
- 第 4 类:1 至 2 σ (10)
- 5 级:2 至 3 σ (9)
- 6 级:3 至 4 σ (2)
- 第 7 类:>=4 σ (1)
作为输出的原始类别需要向读者说明一下。平均数是多少?每个标准偏差的范围是多少?
尽管存在这些不一致,标准偏差类型的地图可能是最合适的地图之一,因为它们的统计来源。所有 4 个字母的国家/地区均 <-1 标准差。有 5 到 8 个字母的国家是 -1 到 0 的标准差。一个 24 个字母的国家/地区超过 4 个标准差,因为它与平均值 8.5 的极端偏差。
漂亮的休息分类
如果您想要范围内的整数,那么您应该选择漂亮的休息时间。所有“漂亮中断”分类所做的就是将每个断点向上或向下舍入。因此,它不会以 599.364 为断点,而是通过漂亮的断点变为 600,000。
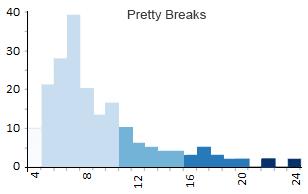
在此示例中很难看出数字的舍入程度(按 5 分组),因为上面的所有示例也产生舍入数。但是当你有像人口估计这样的大数字时(见下文),它会产生一些非常漂亮的中断。
- 1 级:4 – 5 (29)
- 2 级:5 – 10 (111)
- 3 级:10 – 15 (24)
- 4 级:15 – 20 (10)
- 5 级:20 – 24 (2)
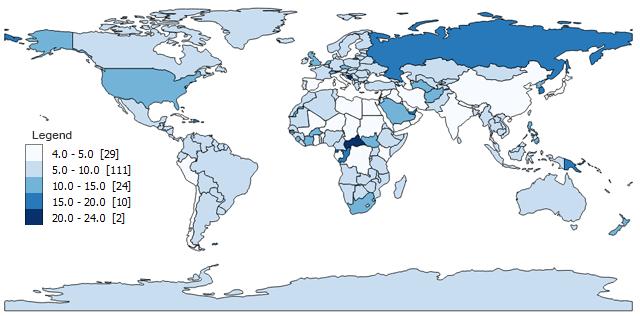
由于制作了四舍五入的数字,漂亮的休息时间也会对您决定的班级数量非常挑剔。
当您查看所有数据分类技术时,人口估计值的比较方式如下:
等间隔:
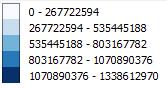
分位数:

自然休息(詹克斯):

漂亮的休息。现在很漂亮:
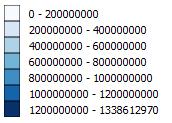
自己试试
等值线图使用不同的阴影和颜色来显示定义区域中的数量或值。
通常情况下,地图制作者使用一种数据分类来制作自己独特的等值线图。每种数据分类方法对读者的影响都不同。
有多种方法可以对 GIS 中的数据进行分类。我们已经通过等值线图的不同示例概述了它们的区别。使用本指南对犯罪率、教育水平和政治等几乎所有事物进行分类。
您最喜欢的数据分类方法是什么?请在下面发表评论让我们知道。