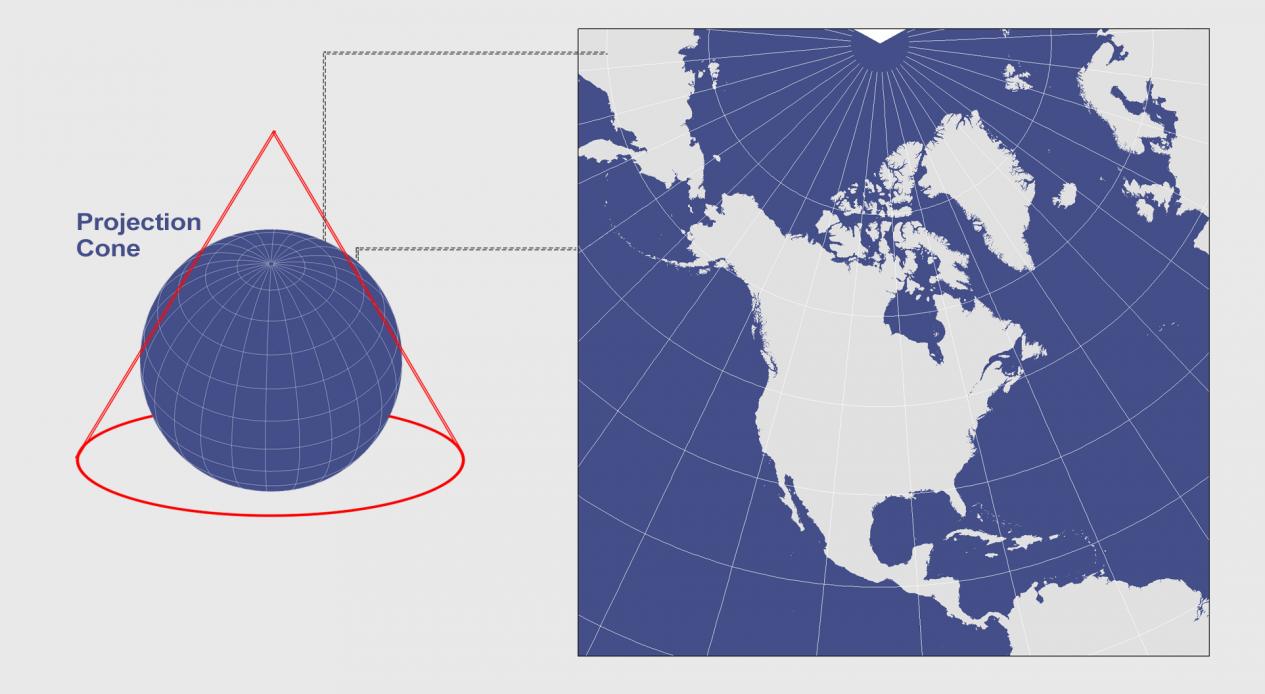
圆锥投影示例
当您在地球上放置一个圆锥体并展开它时,会产生一个圆锥投影。
一些流行的圆锥投影是阿尔伯斯等面积圆锥投影和兰伯特共形圆锥投影。
这两种类型的地图投影都非常适合绘制长东西向区域的地图,因为沿着公共平行线的变形是恒定的。但他们并不擅长投影整个星球。
以下是有关圆锥投影以及当今地图如何使用它们的一些详细信息。
阿尔伯斯等积圆锥投影
阿尔伯斯等面积圆锥投影通常用于显示需要等面积表示的大国。例如,美国地质调查局将此圆锥投影用于显示美国本土(48 个州)的地图。
HC Albers 于 1805 年使用两条标准纬线(割线)引入了这张地图投影。顾名思义,目的是将地图上的所有区域按比例投影到地球上的所有区域。
阿尔伯斯等积圆锥投影畸变
与所有投影一样,Albers Equal Area Conic Projection 具有地图失真。距离和比例仅在方向相当准确的两条标准纬线上都是真实的。面积等于地球上的相同面积,尽管它不是等角的、透视的或等距的。
兰伯特共形圆锥投影
Lambert Conformal Conic 是 Lambert 于 1772 年创作的众多作品之一,至今仍在美国广泛使用。它看起来像阿尔伯斯等面积圆锥曲线,但刻度线间距不同,因此它是共形的而不是等面积的。
它使用两个标准平行线(通常为 33° 和 45°)的圆锥可展曲面正割,以最大限度地减少失真。但是,标准纬线因位置而异。例如,加拿大的标准纬线通常为 49ºN。和 77ºN。
此外,当区域具有东西方向时,美国国家平面坐标系 (SPCS)使用 LCC。
Lambert 共形圆锥投影贴图属性
Lambert Conformal Conic 地图投影的主要优点是它如何保持共形。
尽管距离相当准确并沿标准纬线保持不变,但随着远离标准纬线的失真增加,它的面积并不相等。
多圆锥投影
这种现已过时的地图投影使用与无限数量的平行线相切的无限数量的圆锥体。这种类型的保护通常用于沿纵向范围跨越的国家/地区。
在多圆锥投影中,除中央子午线外的所有子午线都有曲线。只有沿着中央子午线,距离、方向、形状和面积才是真实的。但是,失真会随着远离其中央子午线而增加。
多圆锥投影畸变
总体而言,此地图投影会损害许多属性。它既不是等角的、透视的,也不是等面积的。
圆锥投影的优点和缺点
与圆柱地图不同,圆锥地图投影通常不太适合绘制非常大的区域。它们更适合绘制大陆和区域区域。例如,Albers Equal Area Conic 和 LCC 常用于绘制美国地图。
极坐标圆锥投影的圆锥中心点位于极点正上方。经络笔直汇于极点。纬线是围绕极点的弧线。平行线以直角穿过子午线。
切锥会产生一条标准线,该线上的刻度没有失真。正割锥通过两条标准线减少失真。这些标准线没有失真,但随着远离这些线而增加。
其他资源
以下是一些更有用的地图投影类型参考: