机械臂——六轴机械臂操作空间运动分析
目录
机械臂建模分析:https://blog.csdn.net/Kalenee/article/details/81990130
MoveIt规划下的关节空间运动分析:http://www.guyuehome.com/752
一、简介
在ROS平台下使用MoveIt进行机械臂控制时,默认调用AddTimeParameterization模块完成轨迹的运动规划,输出结果为各关节在对应时间帧下的关节位置与角速度,并没有机械臂末端的运动信息,为此需要通过rosbag完成运动规划的记录并结合Matlab完成操作空间的运动分析。
二、雅可比矩阵
2.1 数学意义
数学上雅可比矩阵(Jacobian matrix)是一个多元函数的偏导矩阵。设有六个拥有六个变量函数如下:
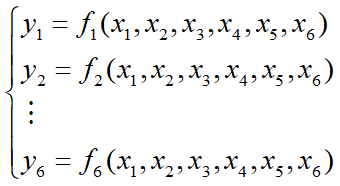
对六个函数微分后得:
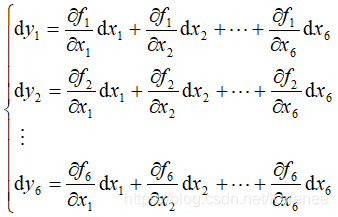
可简写为

其中 为雅可比矩阵,可用J表示。
2.2 机械臂的雅可比矩阵
机械臂的雅可比矩阵J既可表示从关节空间向操作空间的速度传递的线性关系,也可看成是微分运动转换的线性关系。
对于六轴机器人,其雅可比矩阵J(q)是阶矩阵,其中前3行代表对末端线速度V的传递比,后3行代表末端角速度W的传递比,同时矩阵每一列代表对应的关节速度对于末端速度和角速度的传递比, 其中
为对应关节n的单位关节速度,
和
分别为对应关节n的单位关节速度对末端线速度和角速度的影响。
三、操作实现
3.1 记录轨迹
在工作空间下创建bag文件,将记录轨迹的.bag文件及脚本放置在该目录下。
(1)编写节点利用rosbag记录轨迹
rosbag api官方教程:http://wiki.ros.org/rosbag/Code%20API
#include <ros/ros.h>
#include <rosbag/bag.h>
#include <rosbag/view.h>
#include <std_msgs/Bool.h>
#include <std_msgs/Float64MultiArray.h>
#include <string>
#include <trajectory_msgs/JointTrajectory.h>
ros::Subscriber write_sub, motion_sub;
int nums;
bool writeJudge;
rosbag::Bag writeRobot, writePos, writeVel;
void data_process(trajectory_msgs::JointTrajectory getData) {
writeRobot.write("/moveit/JointTrajectory", ros::Time::now(), getData);
for (int j_num = 0; j_num < 6; j_num++) {
std_msgs::Float64MultiArray pos_data, vel_data;
for (int i = 0; i < getData.points.size(); i++) {
pos_data.data.push_back(getData.points[i].positions[j_num]);
vel_data.data.push_back(getData.points[i].velocities[j_num]);
}
writePos.write("pos" + std::to_string(j_num), ros::Time::now(), pos_data);
writeVel.write("val" + std::to_string(j_num), ros::Time::now(), vel_data);
}
}
void write_callback(const std_msgs::Bool::ConstPtr &data) {
if (data->data) {
writeJudge = true;
std::string robotFileName = "bag/motion";
robotFileName += std::to_string(nums);
robotFileName += ".bag";
writeRobot.open(robotFileName, rosbag::bagmode::Write);
std::string posFileName = "bag/motion_pos";
posFileName += std::to_string(nums);
posFileName += ".bag";
writePos.open(posFileName, rosbag::bagmode::Write);
std::string velFileName = "bag/motion_vel";
velFileName += std::to_string(nums);
velFileName += ".bag";
writeVel.open(velFileName, rosbag::bagmode::Write);
} else {
writeJudge = false;
writeRobot.close();
writePos.close();
writeVel.close();
nums++;
}
}
void motion_callback(const trajectory_msgs::JointTrajectory::ConstPtr &data) {
if (writeJudge) {
std::cout << "write" << std::endl;
data_process(*data);
}
}
int main(int argc, char **argv) {
ros::init(argc, argv, "record");
ros::NodeHandle nh;
nums = 1;
writeJudge = false;
write_sub =
nh.subscribe<std_msgs::Bool>("/robot/bagWirte", 1, write_callback);
motion_sub = nh.subscribe<trajectory_msgs::JointTrajectory>(
"/moveit/JointTrajectory", 10, motion_callback);
ros::spin();
}
(2)使用脚本将.bag文件转为.csv文件
创建脚本bagtocsv.sh
#! /bin/bash
echo "Enter bag name"
read bagname
for topic in `rostopic list -b $bagname.bag`;
do rostopic echo -p -b $bagname.bag $topic >$bagname-${topic//\//_}.csv;
echo "finish"
done
cd到该目录下,用bash命令执行,根据提示输入.bag文件的名字。
3.2 轨迹处理
Matlab程序
clear;
%% 前期准备
%启动工具箱
startup_rvc;
%角度转换
du=pi/180; %度
radian=180/pi; %弧度
%关节长度,单位m
L1=0.40;L2=0.39;L3=0.17;L4=0.20;L5=0.08;
%% 建立数学模型
% DH法建立模型,关节角,连杆偏移,连杆长度,连杆扭转角,关节类型(0转动,1移动)
L(1) = Link( 'd',L1 , 'a',0 , 'alpha',-pi/2, 'offset',0 );
L(2) = Link( 'd',0 , 'a',-L2, 'alpha',0 , 'offset',pi/2 );
L(3) = Link( 'd',0 , 'a',0 , 'alpha',pi/2 , 'offset',0 );
L(4) = Link( 'd',L3+L4 , 'a',0 , 'alpha',-pi/2, 'offset',0 );
L(5) = Link( 'd',0 , 'a',0 , 'alpha',pi/2 , 'offset',0 );
L(6) = Link( 'd',L5 , 'a',0 , 'alpha',-pi/2, 'offset',0 );
plotopt = {'noraise', 'nowrist', 'nojaxes', 'delay',0};
tool_char=[1 0 0 0;
0 1 0 0;
0 0 1 0;
0 0 0 1];
six_link=SerialLink(L,'name','six link','tool',tool_char);
%% 显示机械臂
figure('name','机器臂')
hold on
six_link.plot([0 0 0 0 0 0], plotopt{:});
hold off
%% 计算雅可比矩阵
syms theta1 theta2 theta3 theta4 theta5 theta6;
j_trans = six_link.jacob0([theta1 theta2 theta3 theta4 theta5 theta6],'trans');
save('JacobData','j_trans');
%% 读取关节运动参数
%获取关节角度
j1 = csvread('robotMotion_pos-pos0.csv');
j2 = csvread('robotMotion_pos-pos1.csv');
j3 = csvread('robotMotion_pos-pos2.csv');
j4 = csvread('robotMotion_pos-pos3.csv');
j5 = csvread('robotMotion_pos-pos4.csv');
j6 = csvread('robotMotion_pos-pos5.csv');
%获取角速度
j_v = zeros(6,length(j1));
j_v(1,:) = csvread('robotMotion_vel-val0.csv');
j_v(2,:) = csvread('robotMotion_vel-val1.csv');
j_v(3,:) = csvread('robotMotion_vel-val2.csv');
j_v(4,:) = csvread('robotMotion_vel-val3.csv');
j_v(5,:) = csvread('robotMotion_vel-val4.csv');
j_v(6,:) = csvread('robotMotion_vel-val5.csv');
%% 计算末端运动参数
eff_p = zeros(3,length(j1));
eff_v = zeros(3,length(j1));
for i=1:1:length(j1)
theta1 = j1(i);
theta2 = j2(i);
theta3 = j3(i);
theta4 = j4(i);
theta5 = j5(i);
theta6 = j6(i);
% 计算末端位置
eff_p(:,i) = six_link.fkine([theta1 theta2 theta3 theta4 theta5 theta6]).t;
% 计算末端速度
eff_v(:,i) = double(subs(j_trans))*j_v(:,i);
end
%% 画图
time = csvread('robotMotion_time.csv');
hold on;
figure('name','关节空间运动分析')
subplot(2,1,1);
plot(time,j1,time,j2,time,j3,time,j4,time,j5,time,j6);
subplot(2,1,2);
plot(time,j_v(1,:),time,j_v(2,:),time,j_v(3,:),time,j_v(4,:),time,j_v(5,:),time,j_v(6,:));
hold off;
hold on;
figure('name','工作空间运动分析')
subplot(2,1,1);
plot(time,eff_p(1,:),time,eff_p(2,:),time,eff_p(3,:));
subplot(2,1,2);
plot(time,eff_v(1,:),time,eff_v(2,:),time,eff_v(3,:));
hold off;
3.3 结果
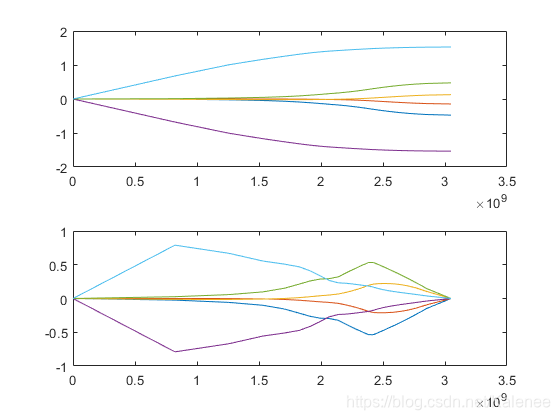
关节空间运动分析
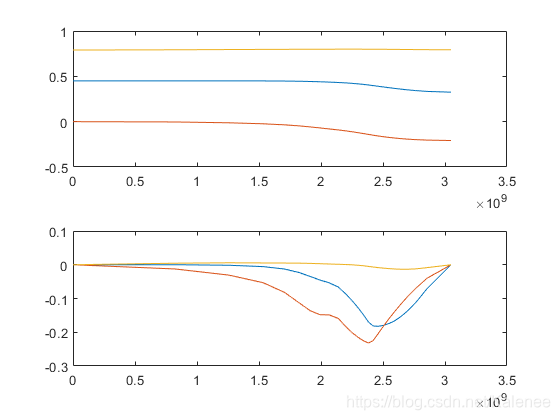
工作空间运动分析
参考:
《机器人技术基础》
转载自:https://blog.csdn.net/Kalenee/article/details/83904997