地理加权回归

空间统计有别于经典统计学的两大特征：空间相关性和空间异质性，莫兰指数等可以用来量化空间相关性，那么地理加权回归，就可以用来量化空间异质性。

在空间上出现的非平稳性，通常被认为由以下三个方面的原因引起的：

• 随机抽样的误差引起的。抽样误差是无法避免的，也是无法观察的，所以统计学上一般只假定它服从某一分布，没必要去死纠这种变化，因为对分析本身的关系作用不大。
• 是由于各地区不同的自然环境、人文环境等差异所引起的变量间的关系随着地理位置的变化而变化。这种变化反应是数据本身的空间特性，所以在空间分析中是需要着重注意的地方。
• 用于分析的模型与实际不符，或者忽略了模型中应有的一些回归变量而导致的空间非平稳性。

• 第一就是所谓的局部回归分析。（比如说按照行政区划）
• 第二就是移动窗口回归。（可以解决边界跳崖式变化）
• 第三就是变参数回归（也就是地理加权回归的前身）

地理加权和其他回归分析一样，首先要划定一个研究区域，当然，通常这个区域也可以包含整个研究数据的全体区域（以此扩展，你可以利用空间关系（比如k-临近），进行局部地理加权计算）……接下去最重要的就是利用每个要素的不同空间位置，去计算衰减函数，这个是一个连续的函数，有了这个衰减函数，当你把每个要素的空间位置（一般是坐标信息（x,y))和要素的值带入到这个函数里面之后，就可以得到一个权重值，这个值就可以带入到回归方程里面去。

地理加权回归里最重要的就是空间权重矩阵。

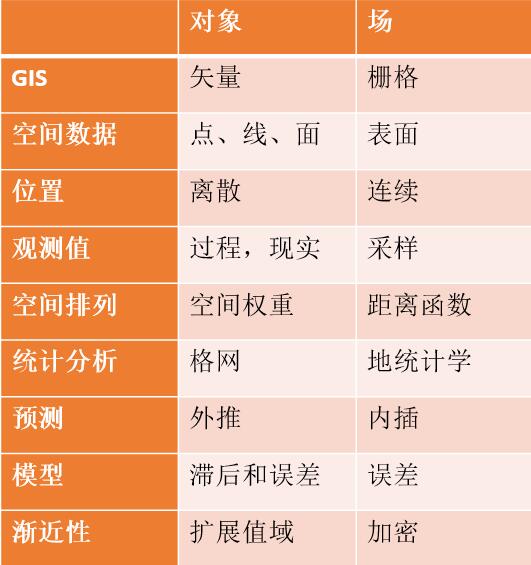
• 空间关系概念化
  空间权重矩阵用是空间关系概念化计算出来的：空间关系观念一共有七个：
  
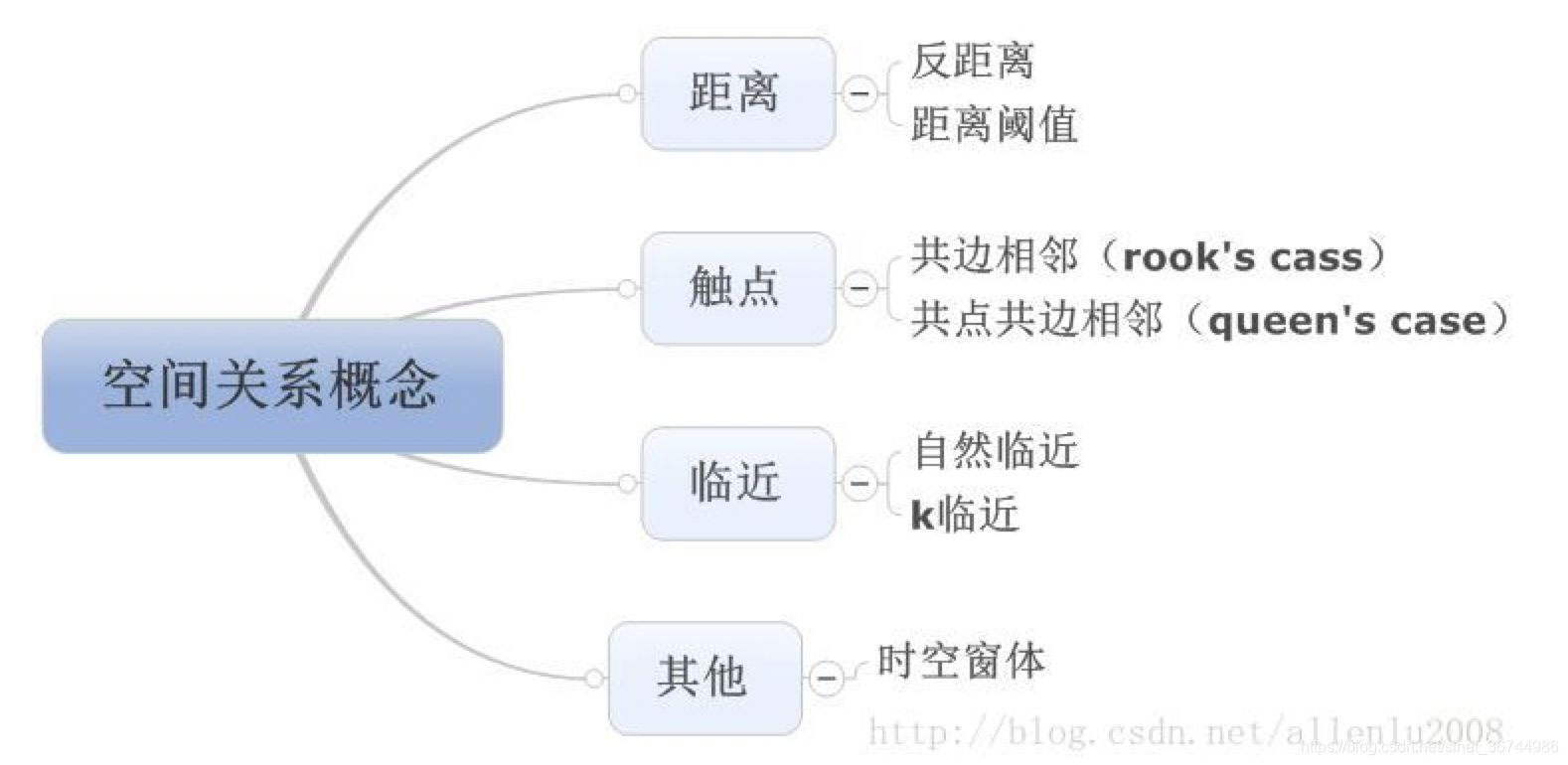
  无论是临近方法，还是触点方法，都会导致局部回归的结果，也就是计算的区间不一样，会导致样本数量的变化，而全部加进来运算，又变成全局回归了，所以在GWR中，能且能够选择的，只有距离方法了。

• GWR中最常用的权函数
  就是选择一个连续单调的递减函数来表示权重w和距离d之间关系，以此来克服反距离的缺点。

  • Gauss函数法

    

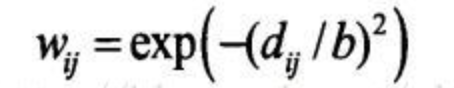
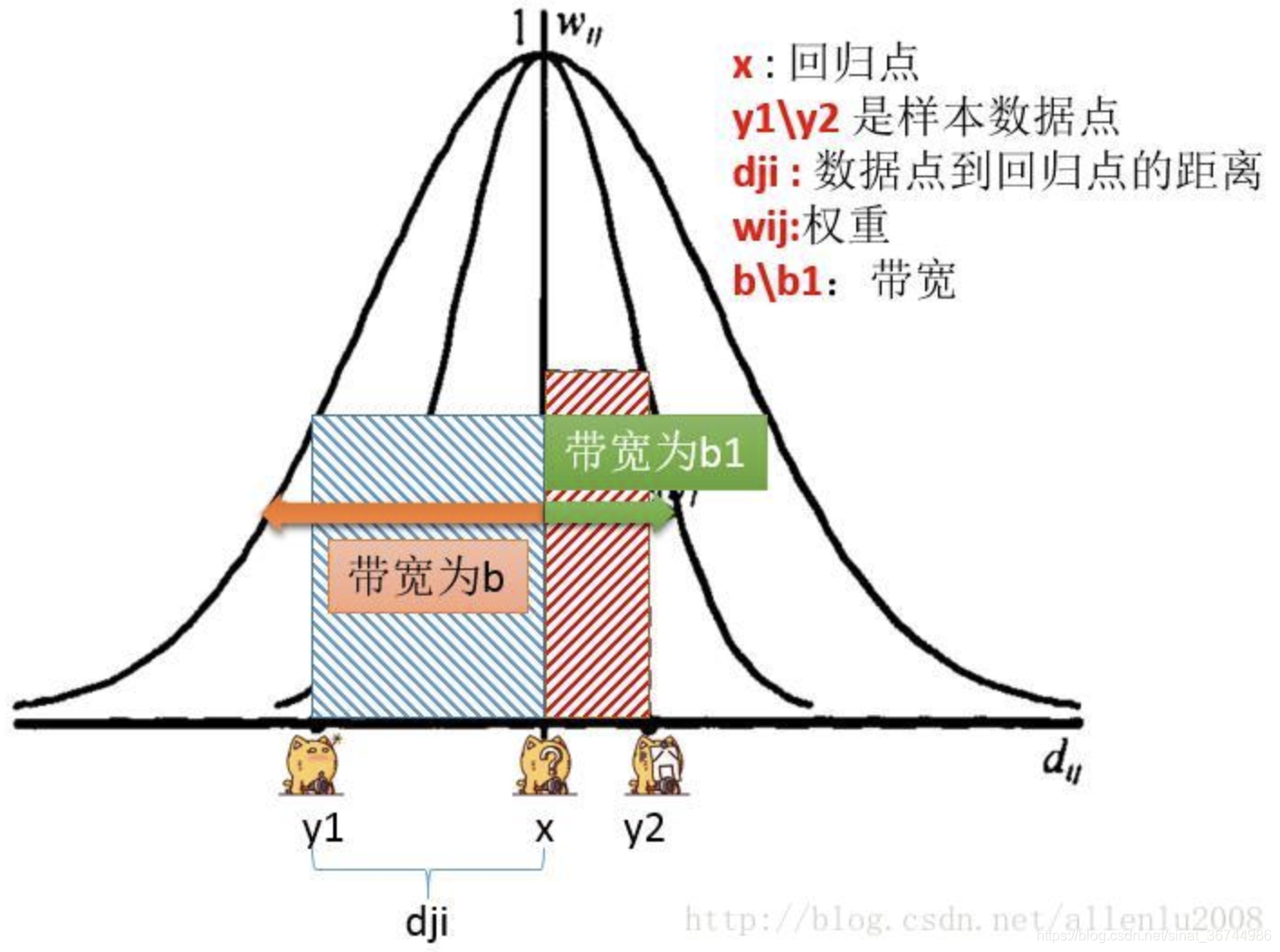其中所谓的带宽b，指的就是权重与距离之间函数关系的非负衰减参数，就像上面那个图所示，带宽越大，权重随距离的增加衰减的越慢，带宽越小，权重随距离的增加衰减的就快。

• 近高斯函数
  但是，如果数据非常离散，带来的结果就是有大量的数据躲得远远的，这种所谓的“长尾效应”会带来大量的计算开销，所以在实际运算中，应用的是近高斯函数来替代高斯计算，把那些没有影响（或者影响很少）的点给截掉，以提高效率。

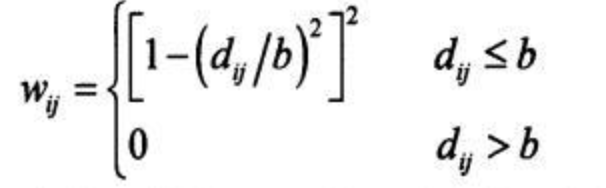
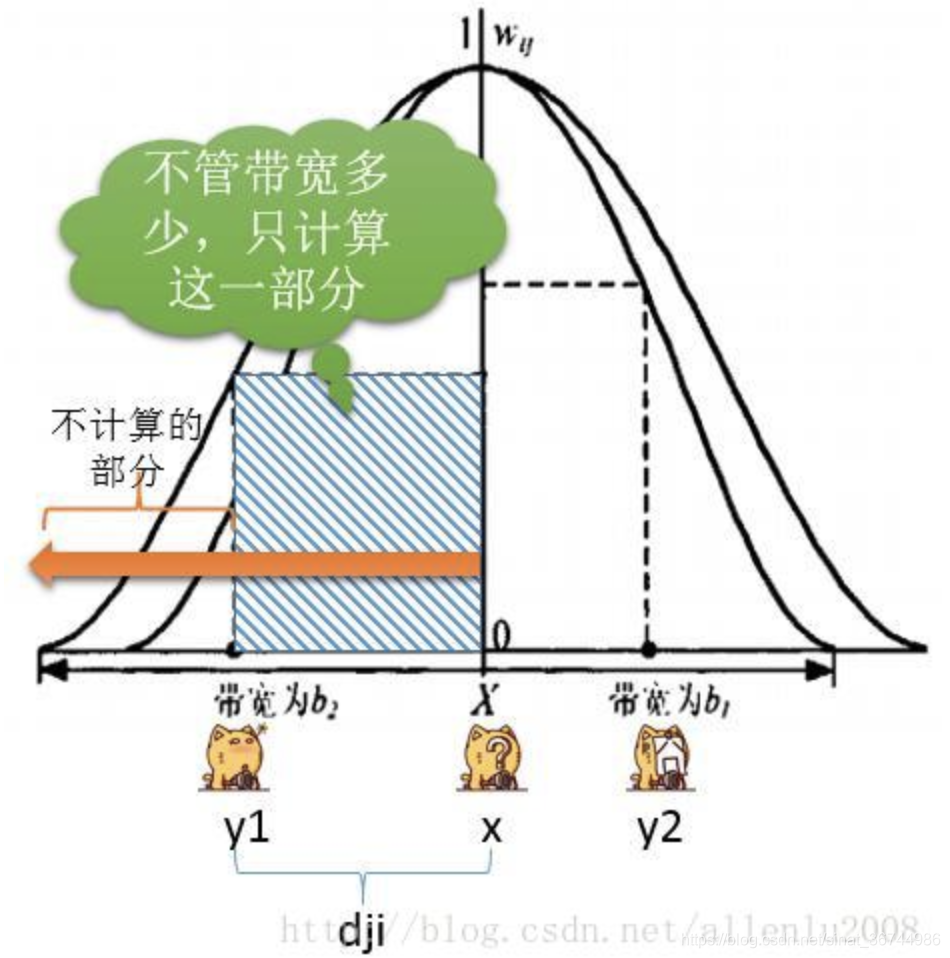
bi-square函数其实是距离阈值法和Gauss函数发法的结合。回归点在带宽的范围内，通过高斯联系单调递减函数计算数据点的权重，超出的部分，权重全部记为0。

地理加权回归对权函数的选择不是很敏感，但是对于带宽的变化却非常敏感。带宽过大会导致回归参数的偏差过大，带宽过小又会导致回归参数的方差过大。

• CV（交叉验证）
  
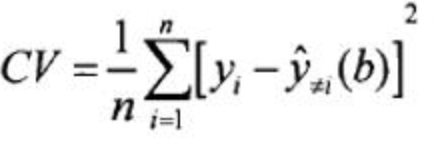
  其中，
  
  表示在回归参数估计的时候，不包括回归点本身，只根据回归点周边的数据进行回归参数计算，然后把不同的带宽和不同的CV绘制成趋势线，那么就可以找出CV值最小的时候，对应的最佳带宽是多少了。

• AIC（最小信息准则）
  

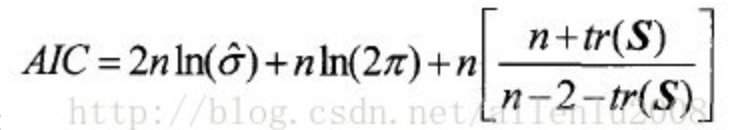
当我们有一堆可供选择的模型参数的时候，选择AIC最小的那个就行……因为AIC的大小取决于独立参数的个数和模型的极大似然函数两个值，参数值少，AIC小，且极大似然函数大，AIC也小，参数少表示模型简洁，极大似然函数大表示模型精确。因此AIC和修正的决定系数类似，在评价模型是兼顾了简洁性和精确性。当两个模型之间存在较大差异的时候，这个差异肯定首先出现在模型的极大似然函数上；而这个函数没有出现显著的差异的时候，模型的独立参数个数才气作用了，从而，参数个数越少的模型，表现得越好。也就是这个原因，这个准则才被称为：最小信息准则。

• Bandwidth 或 Neighbors：是指用于各个局部估计的带宽或相邻点数目，并且可能是“地理加权回归”的最重要参数。它控制模型中的平滑程度。通常，您将通过程序选择所需的带宽值或相邻点值，方法是为带宽方法参数选择修正的 Akaike 信息准则 (AICc) 或交叉验证 (CV)。这两个选项都将尝试识别最佳固定距离或最佳自适应相邻点数目。由于“最佳”条件对于 AICc 和 CV 并不相同，因此通常会获得不同的最佳值。
• ResidualSquares：指模型中的残差平方和（残差为观测所得 y 值与 GWR 模型所返回的 y 值估计值之间的差值）。此测量值越小，GWR 模型越拟合观测数据。此值还在其他多个诊断测量值中使用。（非常重要）
• EffectiveNumber（有效数量）：此值反映了拟合值的方差与系数估计值的偏差之间的折衷，与带宽的选择有关。带宽接近无穷大时，每个观测值的地理权重都将接近 1，系数估计值与全局 OLS 模型的相应值将非常接近。对于较大的带宽，系数的有效数量将接近实际数量；局部系数估计值将具有较小的方差，但偏差将非常大。相反，带宽接近零时，每个观测值的地理权重都将接近零（回归点本身除外）。对于非常小的带宽，系数的有效数量为观测值的数量，局部系数估计值将具有较大方差但偏差较低。该有效数量用于计算多个诊断测量值。
• Sigma：此值为正规化剩余平方和（剩余平方和除以残差的有效自由度）的平方根。它是残差的估计标准差。此统计值越小越好。Sigma 用于 AICc 计算。
• AICc：这是模型性能的一种度量，有助于比较不同的回归模型。考虑到模型复杂性，具有较低 AICc 值的模型将更好地拟合观测数据。AICc 不是拟合度的绝对度量，但对于比较适用于同一因变量且具有不同解释变量的模型非常有用。如果两个模型的 AICc 值相差大于 3，具有较低 AICc 值的模型将被视为更佳的模型。将 GWR AICc 值与 OLS AICc 值进行比较是评估从全局模型 (OLS) 移动到局部回归模型 (GWR) 的优势的一种方法。
• R2：R 平方是拟合度的一种度量。其值在 0.0 到 1.0 范围内变化，值越大越好。此值可解释为回归模型所涵盖的因变量方差的比例。R2 计算的分母为因变量值平方和。向模型中再添加一个解释变量不会更改分母但会更改分子；这将出现改善模型拟合的情况（但可能为假象）。
• R2Adjusted：由于上述 R2 值问题，校正的 R 平方值的计算将按分子和分母的自由度对它们进行正规化。这具有对模型中变量数进行补偿的效果，因此校正的 R2 值通常小于 R2 值。但是，执行此校正时，无法将该值的解释作为所解释方差的比例。在 GWR 中，自由度的有效值是带宽的函数，因此与像 OLS 之类的全局模型相比，校正程度可能非常明显。因此，AICc 是对模型进行比较的首选方式。

参考文献：
1.《白话空间统计：地理加权回归系列》——大虾卢
2.《ArcGIS Desktop 帮助文档》

转载自：https://blog.csdn.net/sinat_36744986/article/details/87864244