半变异函数：Nugget、Range 和 Sill

什么是半变异函数？

托布勒地理学第一定律指出，“一切事物都与其他事物相关，但近处的事物比远方的事物更相关。”

在半变异函数的情况下，更近的事物更容易预测并且变异性更小。而遥远的事物则更难预测，也更不相关。

例如，您前方一米处的地形与 100 米外的地形相似的可能性更大。

正如您将了解到的，半变异函数绘制出样本值（污染、海拔、噪声等）如何随距离变化的这一极其重要的概念。此外，我们将向您展示这与克里金插值的关系。

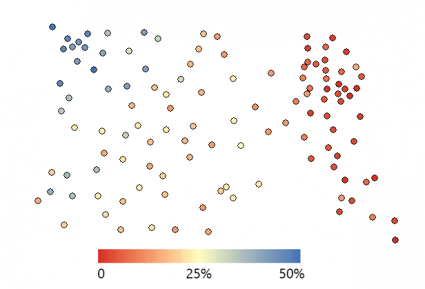
土壤水分样本

我们的示例包含 10 英亩土地中的 73 个土壤水分样本。在西北角，样品更湿润，含水量更高。但在东象限，它们干燥得多，如下图中的颜色编码所示。

不同地方的价值的可预测性如何？
距离更近的已知值是否比距离更远的值更相似？

我们可以用统计依赖或自相关来描述这个想法。此外，空间自相关（距离较近的事物比距离较远的事物更相似）为预测提供了有价值的信息。

半变异函数的工作原理

要了解空间相关性，您可以使用半变异函数对其进行估计。半变异函数采用2 个样本位置并将两点之间的距离称为h 。

在 x 轴上，它以滞后形式绘制距离 (h)，这只是分组的距离。采用每组 2 个样本位置，它测量响应变量（土壤中的含水量）之间的方差并将其绘制在 y 轴上。

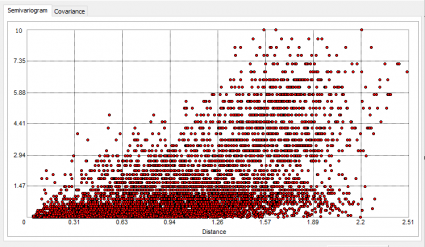
根据观察者的不同，半变异函数看起来像是一堆乱七八糟的点。例如，我们的土壤水分图如下所示：

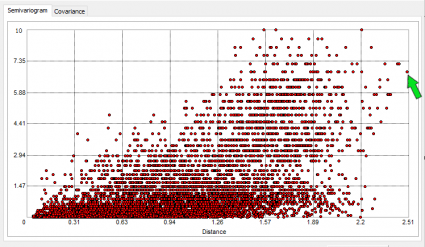
但是你真的可以通过选择个别点来做一些侦探工作。当您在半变异函数上取这个单点时：

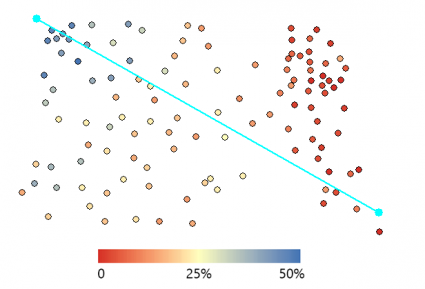
您可以在地图上看到它们代表的是哪 2 个点。这是有道理的，因为它们彼此相距很远。因此，它在半变异函数中的最右边位置。实际上，我们在下面强调这一点：

在特定滞后距离上，它们与平均值也有很大差异。如果半方差较高，则它在 y 轴上的位置较高。正如您可能注意到的那样，半方差在较近的距离处较小，并随着较大的滞后距离而增加。

总记得：

我们正在查看 2 个样本之间的所有距离及其变异性。半变异函数考虑所有点及其距离的方差。这就是为什么半变异函数上有这么多点的原因。这是上面数据集的一个子集，可以看到我们可以在半变异函数中绘制出的所有不同点集。

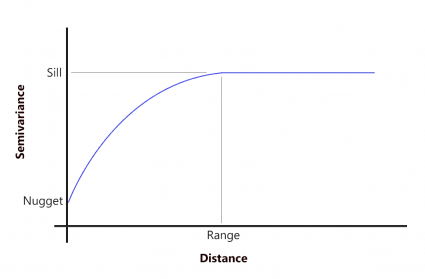
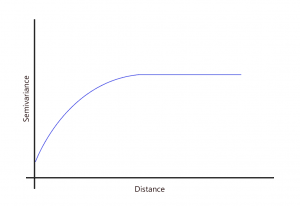
半变异函数中的范围、基台和块金是什么？

在距离较近的样本点处，点之间的值差异往往很小。换句话说，半方差很小。

但当样本点距离较远时，它们不太可能相似。这意味着半方差变大。

随着远离样本点的距离增加，样本点之间不再存在关系。它们的方差开始变平，并且样本值彼此不相关。

SILL ：模型首先变平的值。

范围：模型首先变平的距离。

NUGGET ：半变异函数（几乎）截取 y 值的值。

当您在同一位置有两个样本点时，您可以预期具有相同的值，因此金块应该为零。有时他们不这样做，这增加了随机性。但在图形开始拉平之前，这些值在空间上是自相关的。

正如预期的那样，当距离增加时，半方差增加。相距较远的点对较少，因此样本点之间的相关性较低。

但正如具有基台和范围的半变异函数所示，它开始达到其平坦的渐近水平。这是当您尝试拟合一个函数来模拟这种行为时。

数学函数和模型

您根据模型如何拟合数据来选择模型类型，因为它将为值和距离之间的关系提供数学函数。我们使用最适合的函数，如指数函数、线性函数、球函数和高斯函数。

理想情况下，您正在尝试降低 R 平方值，使其尽可能适合。但是，当您了解现象如何随距离变化时，您可以更好地选择要使用的模型。

例如，以下是可应用于半变异函数的数学函数：

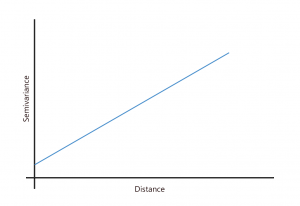
1.线性模型

线性模型意味着空间变异性随距离线性增加。这是最简单的模型类型，没有平台，这意味着用户必须任意选择门槛和范围。

2. 球形模型

球形模型是我们在变差函数建模中最常用的模型之一。它是一个修正的二次方程，其中空间相关性随着基台和范围变平。

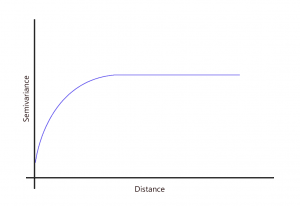
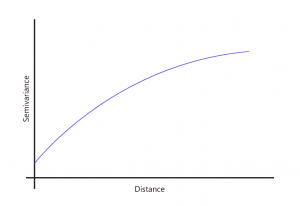
3. 指数模型

指数模型类似于球形模型，因为空间变异性逐渐达到基台。两个样本点之间的关系逐渐衰减，而在无限远的空间依赖性消散。

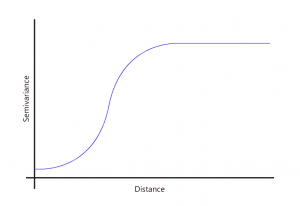
4. 高斯模型

高斯函数使用正态概率分布曲线。这种类型的模型在现象在短距离内相似的情况下很有用，因为它在 y 轴上逐渐上升。

5. 圆形模型

这种类型的预测模型使用循环函数来拟合半变异函数中的空间变异性。它类似于球形模型函数，其中空间依赖性在其渐近水平上逐渐消失。