使用克里金法塑造传奇预测模型
是时候为自己塑造一个时代的预测模型了。克里金法的预测很强。
在创建精细预测表面的过程中,您甚至需要在开始使用克里金法之前了解一些关键概念。
这些概念是什么?
阅读下文以逐步了解克里金法的核心知识。
让我们从一些基础知识开始
要真正理解克里金法,您必须知道插值是什么。与所有插值一样,我们预测其他位置的未知值。
使用像inverse distance weighting这样的插值方法,你可以在不说你有多确定的情况下进行预测。
这是一个例子:
我们通过取最近的三个输入点(12、10 和 10 的值)的反比加权距离来预测紫色点。根据距离,我们计算每个输入点有多远,得到的值为 11.1。
((12/350) + (10/750) + (10/850)) / ((1/350) + (1/750) + (1/850)) = 11.1
这正是确定性插值的工作原理。简单地说,它使用了一个预定义的函数,它就是这样。
但它并没有告诉你你有多确定。
什么是克里金插值?
如果天气预报员预报说明天会下雨,你有多确定明天会下雨?
换句话说:
克里金法不仅会告诉您特定位置的降雨量,还会告诉您特定位置降雨量的概率。
您使用输入数据构建具有半变异函数的数学函数,创建预测表面,然后使用交叉验证来验证您的模型。
地质统计学不仅提供了最佳的预测表面,而且还提供了对预测真实可能性的置信度度量。
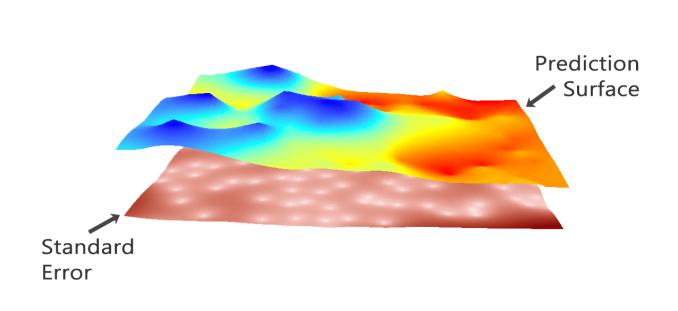
同时,克里金法可以生成预测表面和描述模型预测效果的表面:
预测:该表面直接预测您正在使用克里金法的变量值。
预测错误:它描述了标准错误。当输入数据不多时,您会获得更高的“错误标准”。
概率:概率表面在超过阈值时突出显示。
QUANTILE :该表面以第 99 个百分位数表示最好或最坏的情况。
克里金法的关键是半变异函数
克里金法依赖于半变异函数。简单来说,半变异函数量化自相关,因为它根据距离绘制出所有数据对的方差。
可能是更近的事物更相关并且具有小的半方差。虽然far 事物的相关性较低并且具有较高的半方差。
但在一定距离(范围)内,自相关变得独立。在这种变化趋于平稳的地方,它被称为(sill) 。这意味着数据点的接近度之间不再存在任何空间自相关或关系。这个概念就是托布勒地理第一定律。
同样,这里的目的是拟合一个曲面,例如对整体大规模趋势建模的多项式。然后,围绕该趋势,我们在克里金法出现的地方具有残差的可变性。
根据您的半变异函数结果,您可以选择球形、圆形、指数、高斯或线性的半变异函数。或者,如果你能为一个数学模型做出智力上的证明,那么你就选择那个。
在你开始之前,检查你的数据
在开始克里金法之前,您的数据需要在普通克里金法之前满足这些条件。
如果您的数据满足特定条件,则克里金法是最佳插值技术。但如果它们不符合这些标准,您可以对其进行按摩或完全选择不同的插值技术。
- 您的数据需要呈正态分布
- 数据需要是固定的
- 您的数据不能有任何趋势
以下步骤是检查您的数据以查看它们是否符合这些标准的方法。首先,我们建议绘制出您的点并从低到高对其进行符号化。在我们的示例中,我们使用在农田中采集的土壤水分样本:
假设 1. 您的数据服从正态分布
虽然我们不探索此测试中的空间属性,但我们只是检查值是否呈正态分布。换句话说,您的数据值是否符合钟形曲线形状?
探索这一点的方法之一是使用直方图。在 ArcGIS 中,单击地统计分析 > 探索数据 > 直方图。
此时,您可以检查直方图是否有任何异常值以及它看起来像钟形曲线的程度。在我们的例子中,它看起来具有相当好的正态分布。
或者,您可以使用Normal QQ Plot检查您的数据。正态 QQ 图比较您的数据与正态分布数据的排列方式。如果所有点都呈完全正态分布,则所有点都将落在 45° 线上。在我们的例子中,数据遵循一条直线。
如果您的数据不服从正态分布怎么办?
在这种情况下,您必须应用 Log 或 Arcsin 等变换,直到它变得正常。您可以进行正常分数转换,而不是选择您自己的转换,这几乎可以为您完成很多工作。正态分值变换非常强大,现在作为 ArcGIS 中的简单克里金法,它已成为默认方法。我们将在下面更详细地解释这一点。
假设 2. 您的数据是固定的
您的数据必须是固定的是什么意思?
这意味着局部变化不会在地图的不同区域发生变化。例如,在不同位置相距 5 米的 2 个数据点在您的测量值中应该具有相似的差异。方差在地图的不同区域相当恒定。克里金法不适用于突然变化和断裂线。
您可以使用按熵(邻居之间的变化)或标准差符号化的Voronoi 图检查数据的平稳性,并寻找随机性。在 ArcGIS 中,单击地统计分析 > 探索数据 > Voronoi 地图。
阅读更多: 如何使用泰森多边形绘制 Voronoi 图
在我们的例子中,我们确实看到了一些少量的聚类。总体而言,对于熵和标准偏差,Voronoi 图显示数据集看起来足够平稳。
如果您的数据不稳定怎么办?
经验贝叶斯克里金法 (EBK)可以通过分别处理局部方差来提供帮助。 EBK 不是将方差与整体范围相似,而是在不同区域将克里金法作为单独的基础过程执行。它仍然执行克里金法,但它是在本地完成的。
假设 3. 您的数据没有趋势
趋势是整个研究区域中数据的系统变化。我们可以用ESDA工具查看趋势分析。在 ArcGIS 中,单击地统计分析 > 探索数据 > 趋势分析。
绿线表示东西方向的趋势,蓝线表示南北方向的趋势。通常,我们中心的土壤水分值较高。但是我们的数据中没有足够的趋势需要将其删除。
如果您的数据具有系统趋势怎么办?
尽管整个研究区域中的大趋势可能是完全切换插值方法的原因,但趋势删除工具可以提供帮助,因此后续分析不会受到数据中该趋势的影响。
ArcGIS 中的克里金示例
根据上述条件浏览数据后,您可以单击地统计分析 > 地统计向导。
……现在真正的乐趣开始了,讽刺地说。
步骤 1. 选择克里金法/联合克里金法
现在您已打开地统计向导,克里金法位于地统计方法下。如前所述,这是因为您使用半变异函数构建了最佳预测曲面,并且可以估计该预测为真的可能性的置信度度量。
请注意,如果您选择单个输入,它就是简单的克里金法。但是当你添加第二个变量时,它突然变成了co-kriging 。
如果您有 2 个或更多与山区降水量变化相关的变量,则可以将海拔数据作为协变量添加到降雨量中。在这种情况下,您可以使用辅助信息改进预测。
步骤 2. 选择克里格类型
现在,让我们退后一步,了解所有选项的含义。在这一步中有很多东西需要吸收。
普通克里金法是 ArcGIS 10.0 中的默认设置。现在由于正常分数转换,简单克里金法是默认值。特别是,简单克里金法使用正态分数转换将您的数据转换为标准正态分布。
如前所述,这是执行克里金法的基本条件之一。对于基本用户,最好的选择是采用简单的克里金方法。但存在其他更复杂的克里金类型:
UNIVERSAL KRIGING通过考虑趋势将趋势面分析(漂移)与普通克里金法相结合
INDICATOR KRIGING通过城市和非城市单元格等二进制数据(0 和 1)进行普通克里金法。
PROBABILITY KRIGING使用二进制数据(类似于指示克里金法)并估计一系列截止点的未知点。
最后,您可以在此步骤中手动设置转换类型和趋势移除。例如,如果您想将转换更改为日志,此时您可以进行此更改。
步骤 3. 使用半变异函数对数据建模
在此示例中,我们使用普通克里金法进行演示。地统计向导生成一个带有蓝色十字的半变异函数,显示每对点的平均变异。
滞后大小是位置对分组到的距离类的大小。根据经验,您可以将滞后大小乘以滞后数,使其等于所有点之间最大距离的一半。如果您的点没有聚类,您可以运行“平均最近邻”工具,它会告诉您点之间的平均距离。
ArcMap 添加了为您优化所有这些参数的功能。当您单击优化按钮时,它会找到导致最小均方根误差的每个参数的值。对于用户来说,测试每个场景将需要大量的反复试验。最终,通常最好使用软件认为最佳的半变异函数模型。
对于我们的研究区域,半变异函数如下所示:
第 4 步。使用克里格权重映射模型
在您对拟合的半变异函数感到满意后,向导会提供一个预览表面,其中包含更多参数以自定义输出。克里金法所做的是使用最近邻居的加权平均值来预测每个位置的响应。但首先,您必须设置要在搜索半径中使用的点数(最大和最小)。
尽管关于半变异函数在克里金法中的重要性的讨论如此之多,但此步骤会极大地影响地图的输出。如果更改这些参数中的任何一个,它确实会改变表面的外观和感觉。
如果您选择一种切片扇区类型,这将确保在每个切片中都包含要估计的点。例如,如果您使用四片饼并将邻居设置为 5,则每个切片将使用 5 个点(总共 20 个)进行局部估计。由于没有完美的设定公式,关键是四处移动并检查预测值以了解您认为输出应该是什么样子。
步骤 5. 检查交叉验证结果
克里金法的交叉验证步骤采用您的输入数据点之一并将其从数据集中丢弃。使用所有剩余的点,它将预测运行回该位置。同样,您知道真实值是多少,此过程使用所有剩余值来预测该值。
对于交叉验证,它会遍历所有输入点,直到完成。然后,它会创建这个残差汇总表,将实际值与模型的预测值进行比较。该表显示的是您的模型的真实稳健程度。
那么真实值与预测值有多接近呢?换句话说,您的模型与数据的拟合程度如何?为了正确看待这一切,请检查您的均方根标准化值,因为它应该接近 1。此外,均方根误差应尽可能小。
动态地统计层
因为输出是地统计图层,所以它是动态的,这意味着您可以将其输出类型更改为预测、预测误差、概率或分位数。或者,如果您不喜欢优化的输出,您甚至可以返回到地统计图层并更改参数。
克里金法是一门科学和艺术。
这不仅是您如何从半变异函数中选择模型,而且还包括您如何设置 bin 数量和其他设置。这就是克里格法。
当您表示克里金表面时,例如选择间隔数,它会给结果带来不同的印象。虽然更多的类提供了更多的细节,但数据分类方法(例如分位数或等间隔)以不同的方式排列您的数据。
克里金法的预测很强
空间预测涉及随机性的某些组成部分。当您对数据集进行推断时,这对于地统计学至关重要。
您的克里金权重是根据变异函数估算的。更具体地说,它源自您选择的模型。估计表面的质量反映在权重的质量上。您需要能够给出无偏预测和最小方差的权重。
换句话说,克里金法找到了空间模式。然后它根据该空间模式预测未知值。通过这些预测,克里金法生成误差或不确定性的度量。这意味着您可以估计预测表面的置信度,它们是真实的,而不是因为随机机会。
因为您不仅可以自定义数学函数来构建一个函数,而且还可以使用统计分析的强大功能——即半变异函数。
克里金法是一种地质统计学方法,可根据一组测量值预测地理区域的值。它用于采矿、土壤、地质学和环境科学。
没有一种千篇一律的方法适用于所有人。由于它与您的数据相关,只有您可以决定这些设置是什么以及如何最好地生成预测表面。