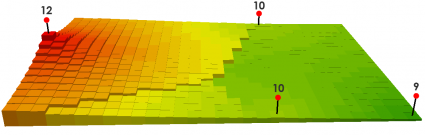
“反距离加权 (IDW) 插值通过指定搜索距离、最近点、功率设置和障碍来估计未知值。”
反距离加权 (IDW) 插值的工作原理
无论您是想估计特定区域的降雨量还是海拔,您都可能想了解不同的插值方法,例如反距离加权。
为此,您从已知值开始,然后通过插值估计未知点。
反距离加权 (IDW) 插值是数学的(确定性的),假设更近的值比更远的值与其函数更相关。
虽然如果您的数据密集且间隔均匀则很好,但让我们看看 IDW 的工作原理以及它最适合的地方。
首先,回顾插值
当给定已知值时,插值会估计未知值。
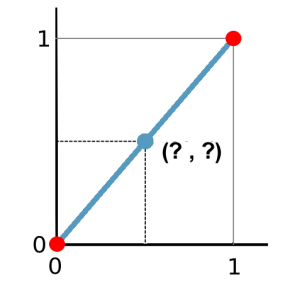
要估计两者之间的点,请在 x 轴上画一条虚线,然后在 y 轴上画一条虚线。蓝点的一个很好的估计是 0.5 和 0.5。你刚刚做了一个线性插值。
GIS 中的插值工作相同。取已知点。通过估计未知表面来创建表面。
空间插值和 IDW
近点比远点更相似:
- 靠近警报器的声音比远离警报器的声音大。
- 下雨时,1 米外比 500 米外更容易下雨。
这些是空间自相关或托布勒地理第一定律的示例。空间自相关是反距离加权的基本假设。
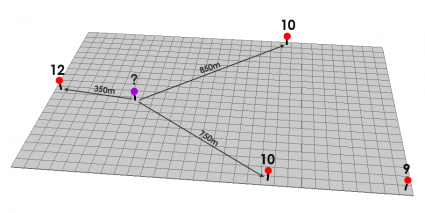
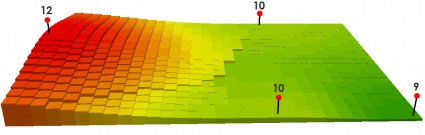
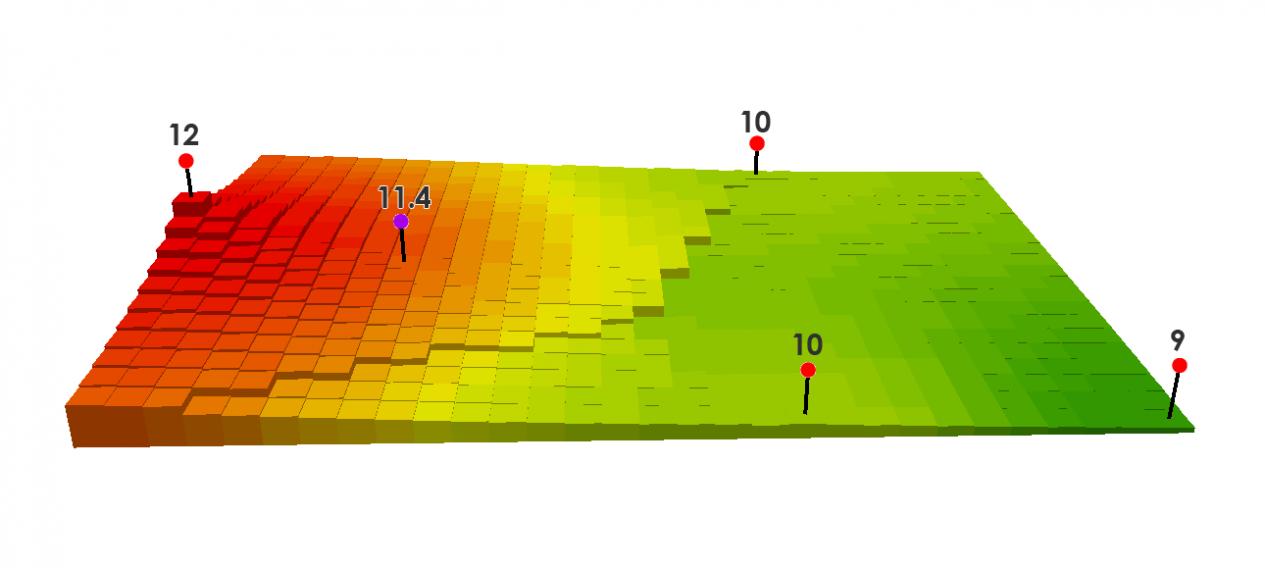
在下面的示例中,红点具有已知的高程值。其他点将被插值。如果您想测量紫色点,您可以设置插值,使其采用固定或可变数量的点。在此示例中,它使用固定数量的点 3 并使用三个最近的点。
您可以看到 IDW 是一种非常灵活的空间插值方法。您可以用不同的方式设置 IDW 插值。
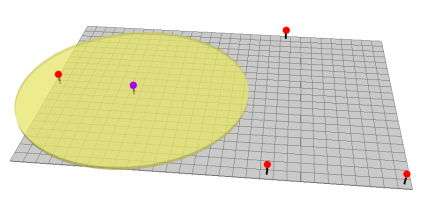
指定您的搜索半径,您的插值将仅使用搜索半径内的已知点数。
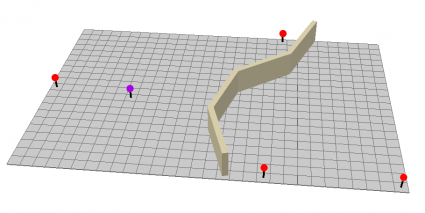
IDW 插值如此灵活的另一个原因是您可以设置障碍。如果海拔剖面或隔音屏障中有山脊——那么这些都是使用屏障的适当示例。此折线障碍阻止它搜索输入样本点。
使用电源设置调整结果
现在,您知道如何设置搜索距离、选择点数和使用障碍,是时候了解 IDW 中的功率设置了。这最好用一个例子来说明。
插值点是根据它们与已知像元值的距离来估计的。与已知值较远的点相比,距离已知值较近的点受到的影响更大。
如果您有1 的幂,它会平滑插值曲面。
如果您有2 的幂,它会增加它对已知值的整体影响。您可以看到峰值和值如何更局部化并且没有像 1 的幂那样平均。
反距离加权背后的数学原理
IDW 数学没有什么好怕的。请记住,搜索距离或最近点的数量决定了将使用多少点。
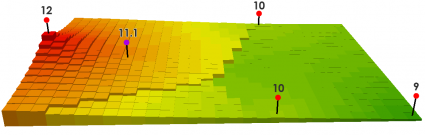
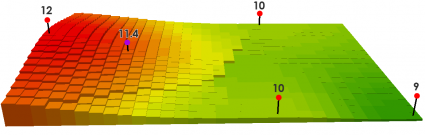
我们在此示例中使用 3 个最近的点:
以下是这 3 个距离和值的表格:
| 距离 | 价值 |
| 350米 | 12 |
| 750米 | 10 |
| 850米 | 10 |
对于1 的幂,该单元格值等于:
((12/350) + (10/750) + (10/850)) / ((1/350) + (1/750) + (1/850)) = 11.1
对于2 的幂,该单元格值等于:
= ((12/350 2 ) + (10/750 2 ) + (10/850 2 )) / ((1/350 2 ) + (1/750 2 ) + (1/850 2 )) = 11.4
……这是公式:
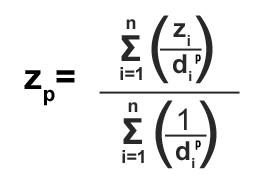
西格玛符号只是意味着您要添加将要插值的任何点数。在这里,我们只是简单地将每个点的高程值相加以获得距离。
分母中的数字越小(距离越远)对插值 (x p ) 值的影响越小。你也永远不会有高于或低于你的最大和最小已知值的值……所以你最好希望你的样本点中有你的最高点或最低点!
尝试插入不同的值。数学真的没那么差!
自己试试
给定一组已知值(例如高程或噪音),您现在可以使用工具来估算您不知道其值的点。
IDW 在其数学中使用空间自相关。越近的值影响越大,而越远的值影响越小。
指定搜索距离或最近点的数量。设置障碍。为更局部的波峰和波谷选择更高的功率设置。
反距离加权插值方法非常灵活。但通常情况下,其他插值技术(如克里金法)可以帮助获得更稳健的模型。