均方根误差 (RMSE) 衡量两个数据集之间存在多少误差。
换句话说,它将预测值与观察值或已知值进行比较。 RMSE 值越小,预测值和观测值越接近。
它也称为均方根偏差,是 GIS 中使用最广泛的统计数据之一。与平均绝对误差 (MAE)不同,我们在比较两个数据集时在各种应用中使用 RMSE。
以下是如何使用 10 个观察值和预测值在 Excel 中计算 RMSE 的示例。但是您可以将相同的计算应用于任何大小的数据集。
什么是均方根误差 (RMSE)?
例如,我们可以将任何预测值与实际测量值(观察值)进行比较。
- 预测值
- 观测值
均方根误差取每个观察值和预测值之间的差值。
您可以交换减法的顺序,因为下一步是求差的平方。这是因为负值的平方始终为正值。但请确保您始终保持相同的顺序。
之后,将所有值的总和除以观察次数。最后,我们得到一个 RMSE 值。 RMSE 公式如下所示:
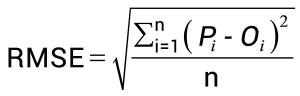
如何在 Excel 中计算 RMSE
这是在 Excel 中计算 RMSE 的快速简便指南。您将需要一组观察值和预测值:
步骤 1. 输入标题
在单元格 A1 中,键入“观察值”作为标题。对于单元格 B1,键入“预测值”。在 C2 中,键入“差异”。
步骤 2. 将值放在列中

如果您有 10 个观测值,请将观测到的高程值放在 A2 到 A11 中。此外,在电子表格的单元格 B2 到 B11 中填充预测值
第 3 步。找出观察值和预测值之间的差异

在 C2 列中,减去观察值和预测值。对下方存在预测值和观察值的所有行重复上述操作。
=A2-B2
现在,这些值可以是正的也可以是负的。
步骤 4. 计算均方根误差值
在单元格 D2 中,使用以下公式计算 RMSE:
=SQRT(SUMSQ(C2:C11)/COUNTA(C2:C11))
单元格 D2 是均方根误差值。并保存你的工作,因为你已经完成了。
如果您有一个较小的值,这意味着预测值接近观察值。反之亦然。
下一步是什么?
RMSE 量化一组值的差异程度。 RMSE 值越小,预测值和观测值越接近。
如果您已经测试过本RMSE 指南,您可以尝试掌握 GIS 中其他一些广泛使用的统计数据:
或者,如果您有任何疑问,请在下面的评论部分告诉我们。