托布勒第一地理定律
一切都与其他一切有关。但是近处的事物比远方的事物更相关。
这是 Waldo R. Tobler 于 1969 年引入的第一条地理学定律。
这个概念适用于污染、噪音、土壤科学和无数现象。
让我们研究两种衡量托布勒地理第一定律的方法。
作为图形的半变异函数
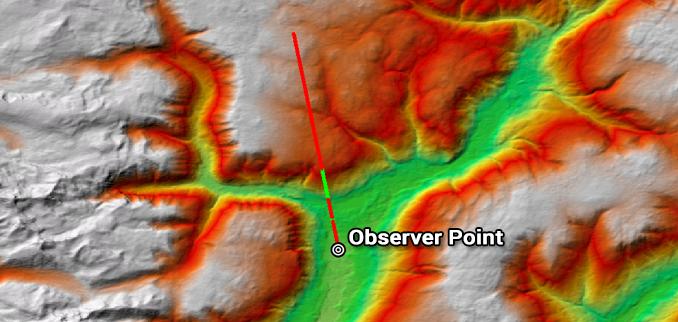
如果再往前看1米,地形高程很可能是一样的。当您朝前方5 米处看时,地面高度会不太相似。但它可能会开始发生变化。现在,当您向100 米远的地方看时,海拔变化更大,以至于它们之间没有关联。
我们在克里格插值中使用半变异函数来理解与距离相关的模式。半变异函数采用2 个样本位置并将点之间的距离表示为h 。
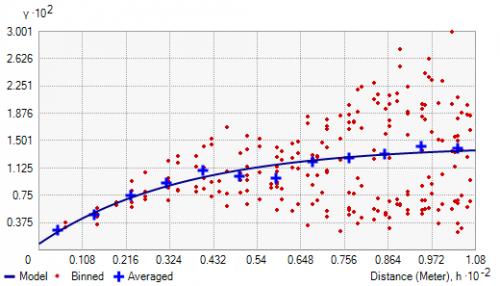
x 轴绘制点之间的距离 (h)。它按滞后对距离进行分组。基于对,它测量响应变量(在 y 轴上)与 x 轴上这两点之间的距离之间的方差。
随着距离的增加,响应变量变得更不可预测且相关性更低。但是对于更近的事物,响应更可预测并且可变性更小。总体而言,半变异函数通过按距离绘制变量图来显示托布勒地理第一定律。
空间自相关和 Moran's I
我们可以用自相关在数值上描述托布勒地理第一定律。空间自相关有助于了解较近的物体与附近其他物体的相似程度。 Moran 指数(或简称为 Moran's I)衡量空间自相关。
我们将 Moran's I 分类为正、负且没有空间自相关。
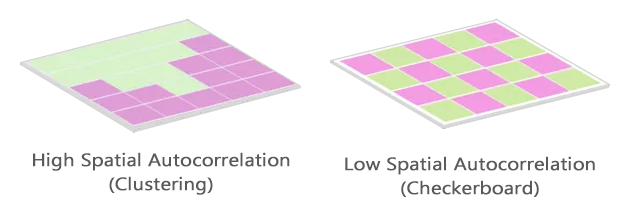
正空间自相关表示地图中的相似值聚类。但负空间自相关表示地图中存在不同的值簇。 Moran's I的值为 0 通常表示没有自相关。
使用空间自相关,地理学家了解疾病和其他现象是否孤立。 Moran's I 可以暗示这种现象正在以分散或聚集的方式传播。
地理第一定律
托布勒地理第一定律基于成本距离或距离衰减。这意味着相距较远的两个地方有更大的阻碍。
例如,如Huff 的引力模型所示,人们不太可能长途跋涉去商店。
随着距离的增加,对运输成本和采购的阻碍就越大。
现在,任何能够描述鲜为人知的地理学第二定律的人都会得到加分。请在下面的评论部分告诉我。