地质统计学的重要性是什么?
地质统计学是一门侧重于空间和时间信息的统计学研究。目的是模拟和发现地理现象的模式。
地质统计学领域涵盖范围广泛的空间统计主题,例如:
- 用于表征数据中空间模式的半变异函数
- 用于空间预测的克里金法
- 衡量非抽样值不确定性的标准误差
地质统计学是一个不断发展的研究领域,我们将其用于采矿、气候研究、土壤科学和大多数环境领域。
为什么要使用地统计学?
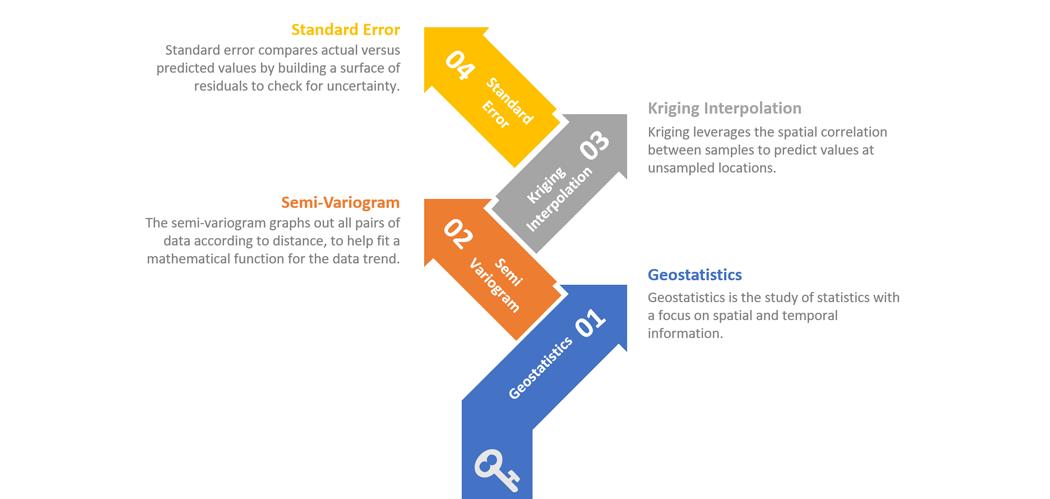
地质统计学提供的三个主要工具是:
- 半变异函数来模拟所有点对之间的关系。
- 克里格建模以预测未采样位置的值。
- 衡量未抽样值置信度的标准误差。
例如,如果您在特定位置有土壤样本,地质统计学可以回答这些类型的问题:
- 未采样位置的土壤水分预测量是多少?
- 土壤水分空间预测的真实可信度有多大?
这与确定性插值技术(如反距离加权 (IDW))不同,后者仅估计未知位置。
通常,IDW 使用预定义的幂函数。那么,结果就是这样。但它并没有告诉你你有多自信。
阅读更多: Kriging Interpolation——这个预测很强
地统计学工具和主题
半变异函数
地质统计学提供半变异函数等描述性工具来识别空间现象的潜在趋势。根据托布勒地理学第一定律,距离较近的事物比距离较远的事物更相关。这也是空间自相关概念的主要思想。
半变异函数根据距离绘制出所有数据对。靠得更近的观察结果具有更高的相关性。但是在一定的距离(范围)内,靠得很近的点之间就不再有关系了。
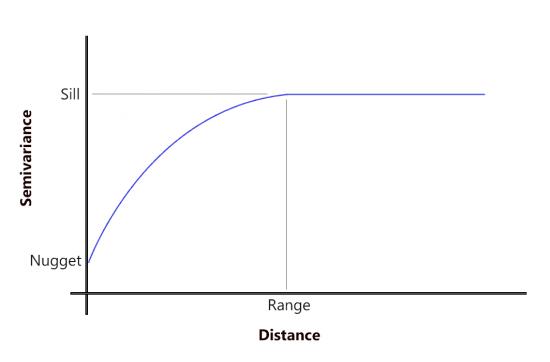
半变异函数描述了这种关系,直到它触及更多样本不再相关的基台。目的是拟合一个数学函数来模拟半变异函数中的趋势。
例如,您可以选择一个半变异函数:
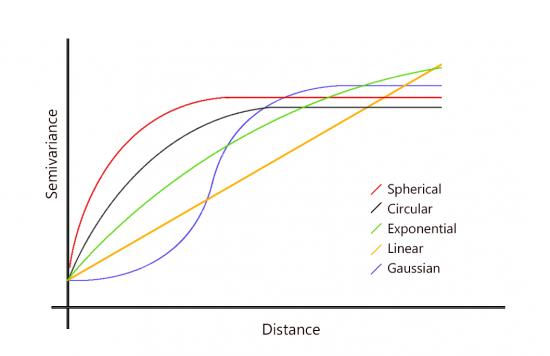
克里格插值
克里金法是一种插值技术,它利用样本之间的空间相关性来预测未采样位置的值。但主要区别在于您可以使用从半变异函数中获得的数学函数来构建它。
以下是地质统计学中可用的不同类型的克里金法:
Co-Kriging添加了第二个相关变量,因此您可以使用辅助信息改进预测。例如,要预测山区的降水量变化,您可以将海拔数据作为协变量添加到降雨量中。
经验贝叶斯克里金法 (EBK)可以通过分别处理局部方差来提供帮助。 EBK 不是在整个范围内具有相似的方差,而是在不同区域将克里金法作为单独的基础过程执行。它仍然执行克里金法,但它是在本地完成的。
Universal Kriging通过考虑趋势在普通克里金法中添加趋势面分析(或漂移)。
Indicator Kriging承载城市和非城市单元格等二进制数据(0 和 1)的普通克里金法。
概率克里金法使用二进制数据(类似于指示克里金法)并估计一系列截止点的未知点。
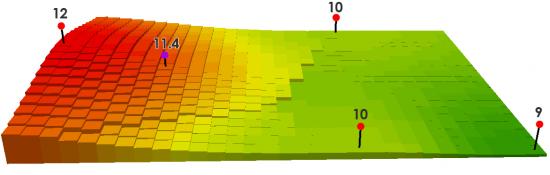
此示例显示了克里金法的空间预测模型。
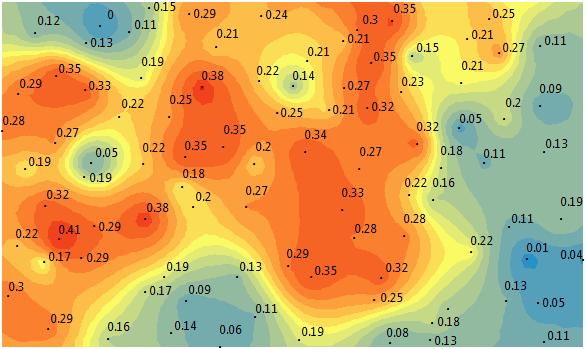
标准误差
地质统计学是有利的,因为它使用标准误差表面图评估未抽样值的不确定性。标准误差图表示预测为真的可能性的置信度度量。
标准误差评估克里格模型的稳健性。通过比较实际值与预测值,它通过构建残差表面来评估不确定性。
一般来说,当你的观察量很少时,你会得到更高的错误标准。当误差超过临界阈值时,专家知识可以为变异函数的过程做出贡献。
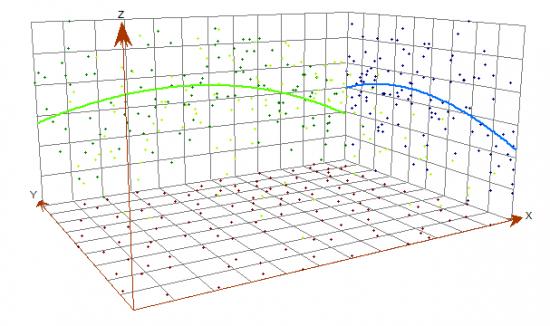
应用和用途
地质统计学最初是为采矿业开发的,用于估算和管理矿石和矿产资源。
但地统计学适用于具有局部变化的各种类型的空间现象。例如,我们使用它来:
- 预测天气、气候、污染和其他大气现象。
- 评估在所有尺度上变化的土壤属性和化学成分。
- 衡量渔业中可持续人口的鱼类丰度。
地质统计学是工程学、地球物理学和大多数自然现象的新兴研究领域。