基于GDAL的OGRPolygon网格化

在使用GDAL做开发的过程中，我需要对有的面进行网格化，如：建筑物面等；在shp文件中建筑物面都是以多边形的形式进行描述的，使用GDAL读取SHP文件中的建筑物面会得到一个个OGRPolygon对象，依据这个对象进行网格化。

需要注意的是，我的这种网格化的方法只针对平面坐标系统有效果，我是基于QT5进行开发的。

首先第一步需要根据多边形建立最大矩形，所以我们需要获得该多边形的最大坐标和最小坐标，从而建立一个最大矩形。

1.获取多边形的外环

OGRLinearRing *poLR = mPolygon->getExteriorRing();

2.分别获取横纵坐标列表

QList<double> x;
	QList<double> y;

	for (int i = 0; i < poLR->getNumPoints(); i++)
	{
		OGRPoint tempPoint;
		poLR->getPoint(i, &tempPoint);
		x.append(tempPoint.getX());
		y.append(tempPoint.getY());
	}

3.给横纵坐标列表进行排序，然后获取最大和最小值

        qSort(x.begin(), x.end());
	qSort(y.begin(), y.end());

	double Xmin = x.first();
	double Ymin = y.first();

	double Xmax = x.last();
	double Ymax = y.last();

然后，根据最大矩形，以给定的长宽进行网格化

       //网格化最大矩形
	QList<double> girdX;
	QList<double> girdY;

	double gx, gy;
	for (gx = Xmin; gx <= Xmax; gx += girdWidth)
	{
		girdX.append(gx);
	}
	gx -= girdWidth;
	if (gx < Xmax) girdX.append(Xmax);

	for (gy = Ymin; gy <= Ymax; gy += girdHeight)
	{
		girdY.append(gy);
	}

	gy -= girdHeight;
	if (gy < Ymax) girdY.append(Ymax);

最后，实例化网格列表，并删除无用的网格

        for (int xIndex = 1; xIndex < girdX.size(); xIndex++)
	{
		for (int yIndex = 1; yIndex < girdY.size(); yIndex++)
		{
			//OGRPoint minPoint(girdX[xIndex-1],girdY[yIndex-1]);
			//OGRPoint maxPoint(girdX[xIndex],girdY[yIndex]);
			//qDebug() << xIndex - 1 << yIndex - 1 << xIndex << yIndex;

			OGRPoint lbottomPoint(girdX[xIndex - 1], girdY[yIndex - 1]);
			OGRPoint ltopPoint(girdX[xIndex - 1], girdY[yIndex]);
			OGRPoint rtopPoint(girdX[xIndex], girdY[yIndex]);
			OGRPoint rbottomPoint(girdX[xIndex], girdY[yIndex-1]);

			OGRPolygon  *tempPolygon = new OGRPolygon;  //多边形
			OGRLinearRing *mLineRing = new OGRLinearRing;  //多边形中的ring
			mLineRing->addPoint(&lbottomPoint);
			mLineRing->addPoint(<opPoint);
			mLineRing->addPoint(&rtopPoint);
			mLineRing->addPoint(&rbottomPoint);
			tempPolygon->addRingDirectly(mLineRing);
			tempPolygon->closeRings();

			//筛选网格，求交叉
			OGRPolygon *iPolygon =(OGRPolygon*)mPolygon->Intersection(tempPolygon);
			OGRLinearRing *plRing = iPolygon->getExteriorRing();
			if (plRing != nullptr)
			{
				double mArea = iPolygon->get_Area();
				qDebug() << mArea;
				int num = plRing->getNumPoints();
				QPolygonF mPolygonF;
				for (int i = 0; i < num; i++)
				{
					OGRPoint mPoint;
					
					plRing->getPoint(i, &mPoint);
					QPointF mPointf(mPoint.getX(), mPoint.getY());
					mPolygonF.append(mPointf);
				}
				tempGirdList.append(mPolygonF);
				//qDebug() << mPolygonF;
			}	
		}
	}

网格化示例图

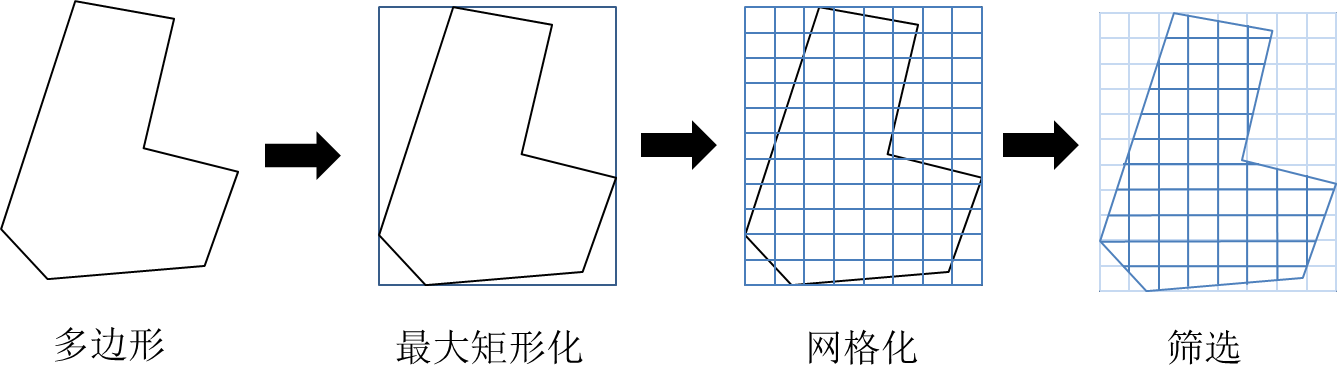
以下是全部代码示例

QList<QPolygonF> LayerOper::girdPolygon(OGRPolygon *mPolygon, double girdWidth, double girdHeight)
{
	//获取最小和最大坐标，建立最大矩形
	QList<QPolygonF> tempGirdList;
	OGRLinearRing *poLR = mPolygon->getExteriorRing();

	QList<double> x;
	QList<double> y;

	for (int i = 0; i < poLR->getNumPoints(); i++)
	{
		OGRPoint tempPoint;
		poLR->getPoint(i, &tempPoint);
		x.append(tempPoint.getX());
		y.append(tempPoint.getY());
	}

	qSort(x.begin(), x.end());
	qSort(y.begin(), y.end());

	double Xmin = x.first();
	double Ymin = y.first();

	double Xmax = x.last();
	double Ymax = y.last();

	//网格化最大矩形
	QList<double> girdX;
	QList<double> girdY;

	double gx, gy;
	for (gx = Xmin; gx <= Xmax; gx += girdWidth)
	{
		girdX.append(gx);
	}
	gx -= girdWidth;
	if (gx < Xmax) girdX.append(Xmax);

	for (gy = Ymin; gy <= Ymax; gy += girdHeight)
	{
		girdY.append(gy);
	}

	gy -= girdHeight;
	if (gy < Ymax) girdY.append(Ymax);

	for (int xIndex = 1; xIndex < girdX.size(); xIndex++)
	{
		for (int yIndex = 1; yIndex < girdY.size(); yIndex++)
		{
			//OGRPoint minPoint(girdX[xIndex-1],girdY[yIndex-1]);
			//OGRPoint maxPoint(girdX[xIndex],girdY[yIndex]);
			//qDebug() << xIndex - 1 << yIndex - 1 << xIndex << yIndex;

			OGRPoint lbottomPoint(girdX[xIndex - 1], girdY[yIndex - 1]);
			OGRPoint ltopPoint(girdX[xIndex - 1], girdY[yIndex]);
			OGRPoint rtopPoint(girdX[xIndex], girdY[yIndex]);
			OGRPoint rbottomPoint(girdX[xIndex], girdY[yIndex-1]);

			OGRPolygon  *tempPolygon = new OGRPolygon;  //多边形
			OGRLinearRing *mLineRing = new OGRLinearRing;  //多边形中的ring
			mLineRing->addPoint(&lbottomPoint);
			mLineRing->addPoint(<opPoint);
			mLineRing->addPoint(&rtopPoint);
			mLineRing->addPoint(&rbottomPoint);
			tempPolygon->addRingDirectly(mLineRing);
			tempPolygon->closeRings();

			//筛选网格，求交叉
			OGRPolygon *iPolygon =(OGRPolygon*)mPolygon->Intersection(tempPolygon);
			OGRLinearRing *plRing = iPolygon->getExteriorRing();
			if (plRing != nullptr)
			{
				double mArea = iPolygon->get_Area();
				qDebug() << mArea;
				int num = plRing->getNumPoints();
				QPolygonF mPolygonF;
				for (int i = 0; i < num; i++)
				{
					OGRPoint mPoint;
					
					plRing->getPoint(i, &mPoint);
					QPointF mPointf(mPoint.getX(), mPoint.getY());
					mPolygonF.append(mPointf);
				}
				tempGirdList.append(mPolygonF);
				//qDebug() << mPolygonF;
			}	
		}
	}
	return tempGirdList;
}

经过测试，我发现了一个BUG,多怪我考虑得不够细致，按照上面的多边形划分的方法，可能会出现下面这种情况：

如红色标记的网格，它与多边形的交叉部分有两个区域，所以上面的写法就不正确了，那只获取了一个多边形的区域，要获取多个交叉区域怎么办呢？看下面代码：

OGRGeometry *pRet = mPolygon->Intersection(tempPolygon);
			if (pRet != NULL)
			{
				OGRwkbGeometryType pGeoType = pRet->getGeometryType();
				if (pGeoType == wkbPolygon)//这里就是多边形判断
				{
					OGRPolygon *rdPolygon = (OGRPolygon*)pRet->clone();
					QPolygonF mPolygonF;
					bool ret = ogrPolygon2qpolygonf(rdPolygon, mPolygonF);
					if (ret)
					{
						tempGirdList.append(mPolygonF);
					}
				}
				else if (pGeoType == wkbMultiPolygon)  //这里是多个相交区域获取方法
				{
					OGRMultiPolygon * multiPolygon = (OGRMultiPolygon *)pRet;
					int num = multiPolygon->getNumGeometries();
					for (int i = 0; i < num; i++)
					{
						OGRPolygon *mOGRPolygon = (OGRPolygon *)multiPolygon->getGeometryRef(i);
						QPolygonF mPolygonF;
						bool ret = ogrPolygon2qpolygonf(mOGRPolygon, mPolygonF);
						if (ret)
						{
							tempGirdList.append(mPolygonF);
						}
					}
				}
			}

我把OGRPolygon转QPolygon类型封装成了一个函数：

bool LayerOper::ogrPolygon2qpolygonf(OGRPolygon *mPolygon, QPolygonF &targetPolygon)
{
	OGRLinearRing *plRing = mPolygon->getExteriorRing();
	if (plRing != nullptr)
	{
		int num = plRing->getNumPoints();
		for (int i = 0; i < num; i++)
		{
			OGRPoint mPoint;

			plRing->getPoint(i, &mPoint);
			QPointF mPointf(mPoint.getX(), mPoint.getY());
			targetPolygon.append(mPointf);
		}
		return true;
	}
	else
	{
		return false;
	}
}

欢迎大家指正！

转载自：https://blog.csdn.net/octdream/article/details/77097909