利用PostGIS实现求解点集的最小面积包围矩形

最近，空间数据库原理课上涉及到利用PostGIS求解点集的最小面积包围矩形的问题，记录在此，希望能帮助到有需要的人。第一次写博客，有什么错误希望见谅。
本方法的实现原理为：最小面积外接矩形的一条边肯定与点集的凸包的一条边重合，所以思路为遍历凸包的每条边，构造外接矩形，计算面积，找出面积最小的那个外接矩形即可。

一、 建立一个multipnt表用于保存测试数据

CREATE TABLE multipnt(
gid serial,
geom geometry
);

二、 输入三条测试数据

INSERT INTO multipnt(geom) VALUES
(ST_GeomFromText('MULTIPOINT(50 5, 100 70, 50 20, 30 10,70 400)')),
(ST_GeomFromText('MULTIPOINT(145 35, 200 50, 276 300)')),
(ST_GeomFromText('MULTIPOINT(350 5, 450 78, 370 20, 320 108,540 400,325 87)'));

三、 利用ST_ConvexHull函数建立多点要素的最小凸多边形并将其转化成线环，将结果放入到视图ch_polygon中

CREATE OR REPLACE VIEW ch_polygon AS(
SELECT gid,ST_Boundary(ST_ConvexHull(geom)) AS geom
FROM multipnt
);

创建的最小凸多边形转换成线环，在QGIS中显示如下

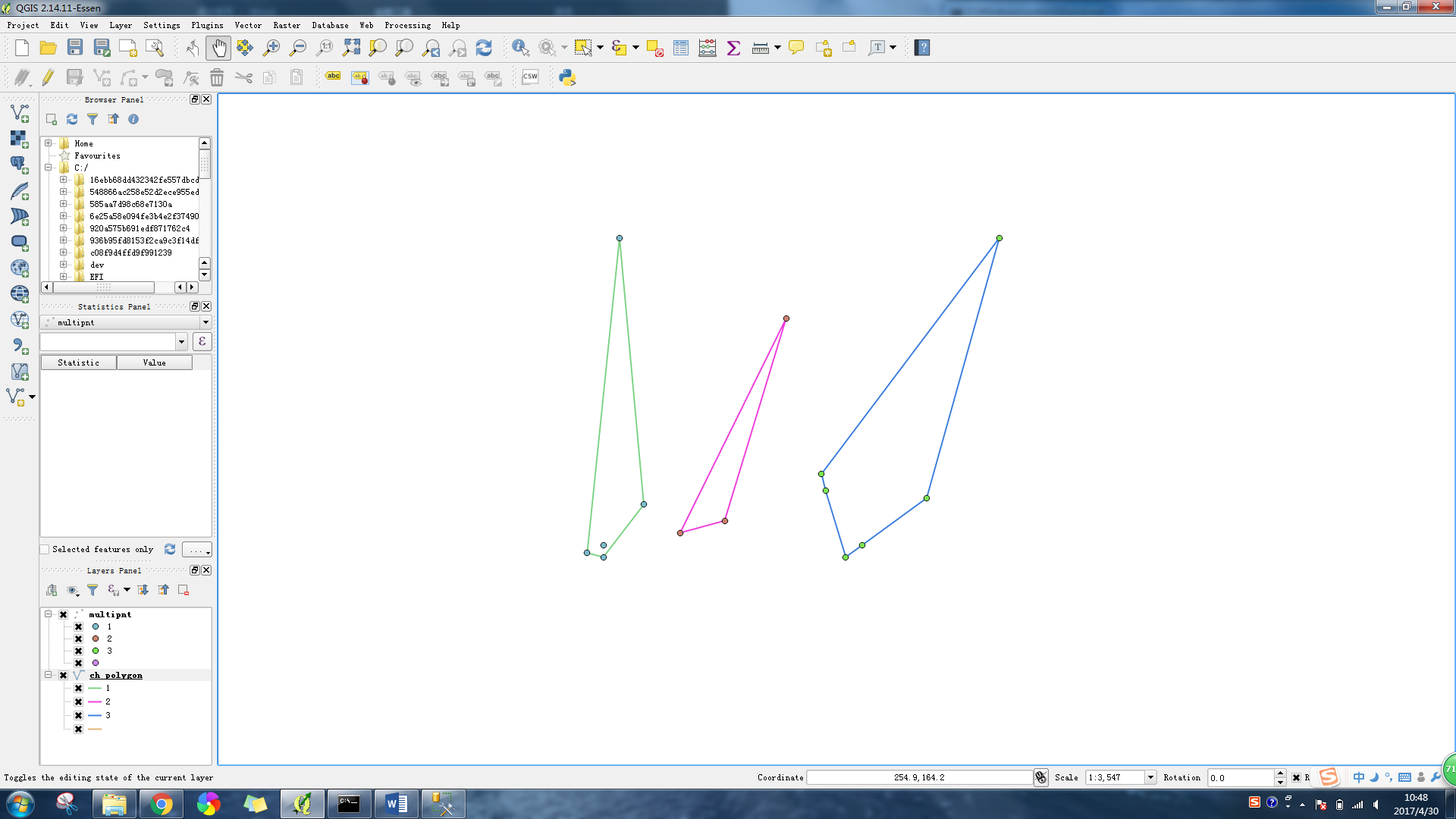
四、 创建最小包围矩形
1、 将每个多边形的每条边取出来用起点终点表示，放在新建的视图edges中，用于后面计算每条边的方位角。（外接矩形的长宽的计算要根据各个点在某一条边上的投影来确定，但是投影的计算比较复杂，所以可以将多边形进行旋转，依次让一条边和x轴平行，这样的话，最小外接矩形的长宽即分别为各点xy的最大值与最小值之差，构造出最小外接矩形后，再将构造出来的矩形按照前面旋转的反方向进行旋转，就可以得到最小外接矩形）

CREATE OR REPLACE VIEW edges AS(
WITH RECURSIVE x(gid,n,pnt_num) AS(
SELECT gid,1 AS n,ST_NumPoints(geom) AS pnt_num
FROM ch_polygon
UNION ALL
SELECT gid,n+1,pnt_num
FROM x
WHERE n<pnt_num-1
)
SELECT gid,n AS eid,ST_PointN(geom,n)AS from_pnt,
ST_PointN(geom,n+1)AS to_pnt,geom FROM
(
SELECT x.gid,n,geom FROM x INNER JOIN ch_polygon p ON(x.gid=p.gid)
) AS a
);

2、 计算每个多边形的每条边的方位角，然后将多边形进行旋转使得每个多边形分别与自己的每条边平行，以便于计算其他边在这条边上的投影，将所得的结果存放在新视图rotate_polygon中

CREATE OR REPLACE VIEW rotate_polygon AS(
WITH t AS(
SELECT gid,eid,3*PI()/2+ST_Azimuth(from_pnt,to_pnt)AS angle,geom
FROM edges
)
SELECT gid,eid,ST_Rotate(geom,angle)AS geom,angle
FROM t
);

在QGIS中显示图形如下所示，可以看到每个旋转后的多边形都有一条边与x轴平行。

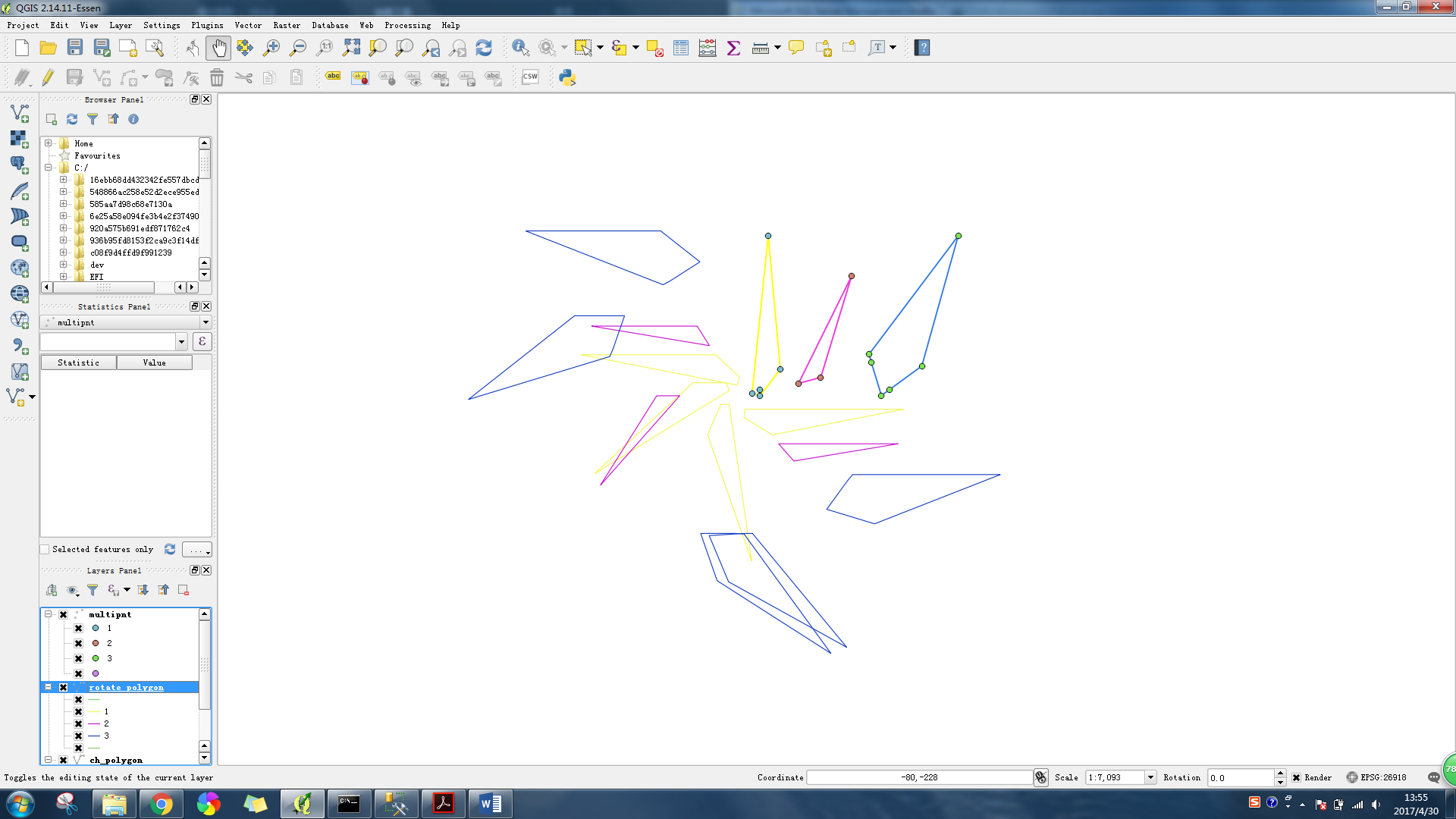
3、 将rotate_polygon中的每个线串的x、y的最大最小值，并将结果放在新视图pnt_exterma

CREATE OR REPLACE VIEW pnt_exterma as(
WITH RECURSIVE x(gid,eid,n,pnt_num) AS(
SELECT gid,eid,1 AS n,ST_NumPoints(geom) AS pnt_num
FROM rotate_polygon
UNION ALL
SELECT gid,eid,n+1,pnt_num
FROM x
WHERE n<pnt_num-1
)
SELECT gid,eid,MIN(ST_X(geom))AS minx,MIN(ST_Y(geom))AS miny,
MAX(ST_X(geom))AS maxx,MAX(ST_Y(geom))AS maxy 
FROM(
SELECT r.gid,r.eid,n,ST_PointN(geom,n)AS geom
FROM rotate_polygon r
INNER JOIN x ON(r.gid=x.gid and r.eid=x.eid)
)AS a
GROUP BY a.gid,a.eid ORDER BY gid,eid
);

4、 利用pnt_exterma视图中的数据，计算由x、y的最大最下值形成的各个矩形的面积，求出最小值，即是最小矩形，将结果存放在视图min_rect中。

CREATE OR REPLACE VIEW min_rect AS(
SELECT * FROM(
WITH t AS(
SELECT gid,eid,ST_MakeEnvelope(minx,miny,maxx,maxy)AS geom,
(maxx-minx)*(maxy-miny) AS area 
FROM pnt_exterma
)
SELECT gid,eid,geom,area,
RANK() OVER(PARTITION BY gid ORDER BY area) AS area_rank 
FROM t
)AS a
WHERE area_rank=1
);

在QGIS中显示结果如下图所示

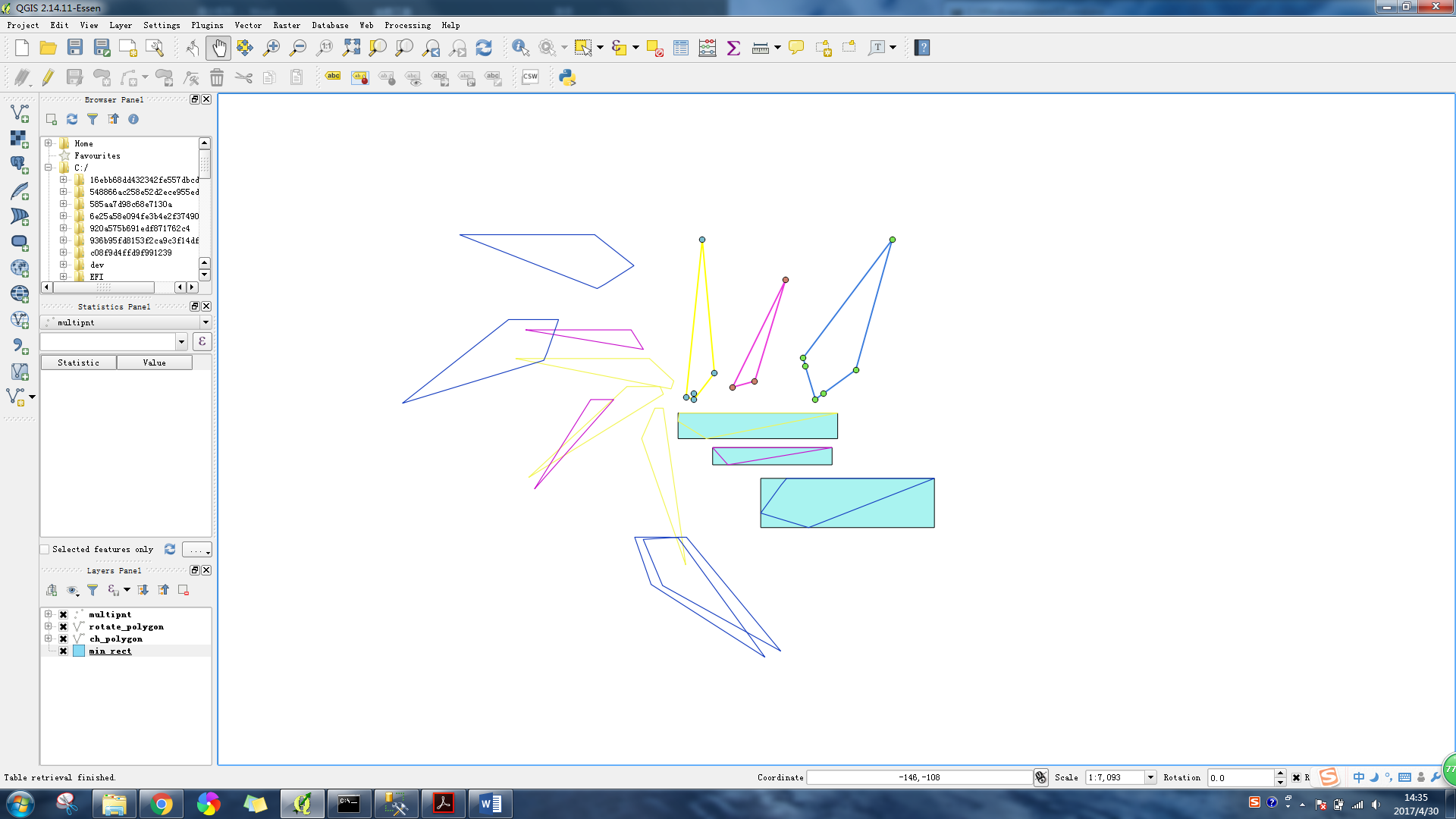
5、 将min_rect中的矩形进行旋转，最后得到点集的面积最小的包围矩形，将结果放入新视图result中

CREATE VIEW result AS(
WITH t AS(
SELECT m.gid,angle 
FROM min_rect m,rotate_polygon p
WHERE m.gid=p.gid AND m.eid=p.eid
)
SELECT min_rect.gid,area,ST_Rotate(geom,-angle)AS geom 
FROM min_rect,t
WHERE min_rect.gid=t.gid
);

在QGIS中显示结果如下图所示，点集的面积最小的包围矩形得以求解。

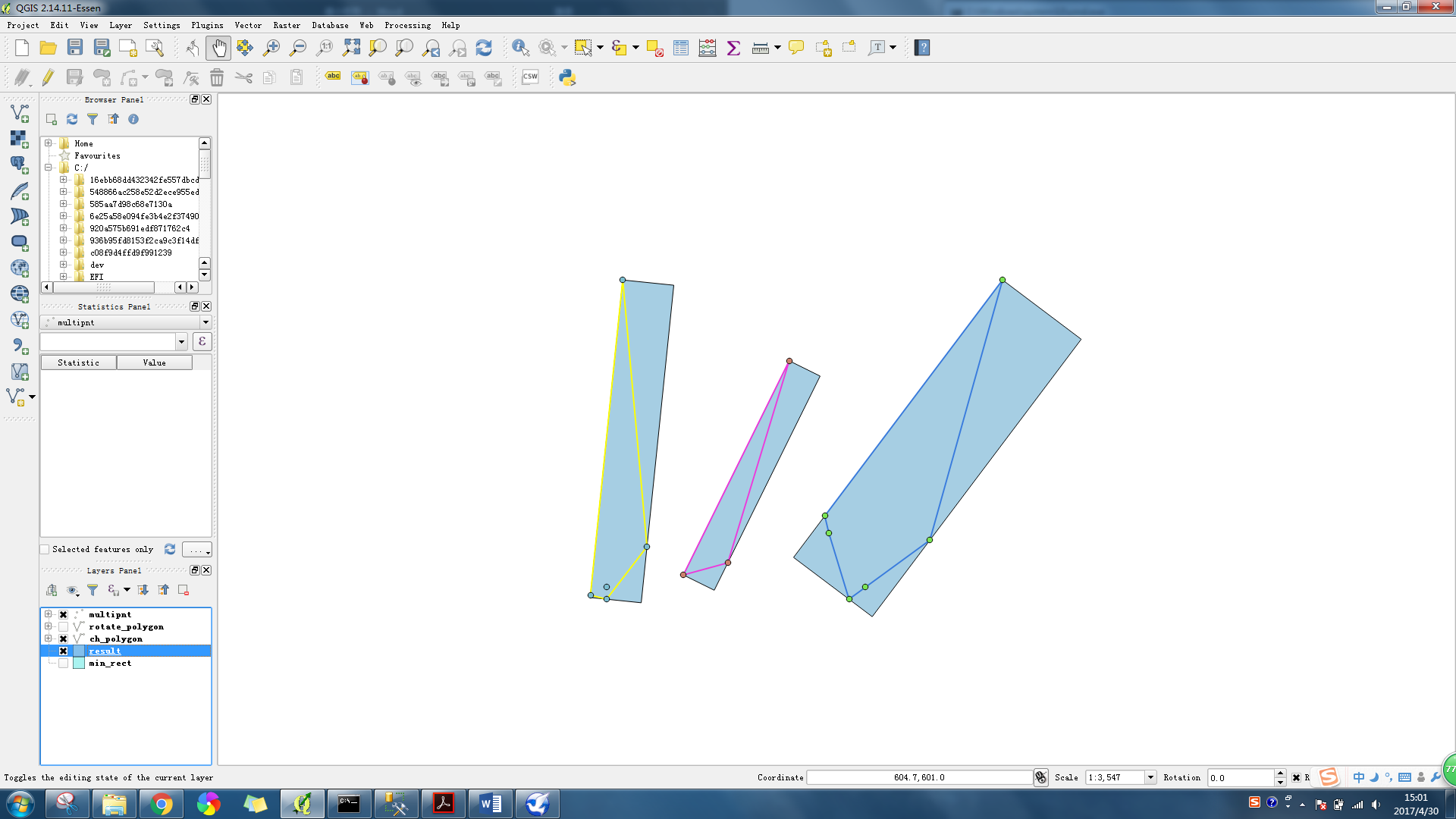
其面积在属性表中显示如下：

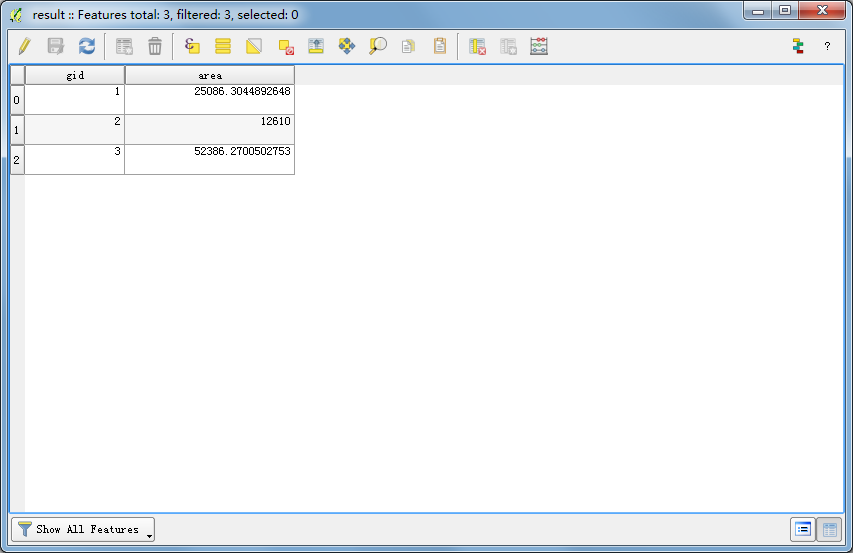
转载自：https://blog.csdn.net/qq_31709249/article/details/71102258