矢量数据压缩，道格拉斯——普克法算法实现

这里矢量数据压缩是指线的数据压缩，意思是假如某根线有n个点，现在如果删除一些点，这条线仍然性质良好，那么就实现了压缩，那么下面的算法目的就是对线上不必要一些点给删除了。

算法名字叫道格拉斯——普克法算法，当然还有还有其他算法，学习这个算法原因是它使用了递归，其实很早以前就尝试写这个算法，无奈当时只会些顺序循环之流，苦闷数日不得其解，如今终有机会手刃此题，甚欢！

算法描述：
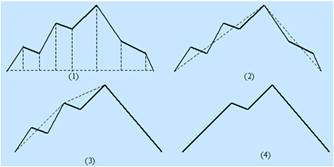
对每一条曲线的首末点虚连一条直线，求所有点与直线的距离，并找出最大距离值dmax，用dmax与限差D相比：
若dmax＜D，这条曲线上的中间点全部舍去；
若dmax≥D，保留dmax对应的坐标点，并以该点为界，把曲线分为两部分，对这两部分重复使用该方法。

纯C代码：

#include <stdio.h>
#include <stdlib.h>
#include <math.h>

typedef struct//点的数据结构
{
    double x;
    double y;
    int tag;//判断此点是否保留标志，1保留，0不保留
}Point;


///getmax是获取最大距离与最大距离所对应点标号函数
void getmax(double *dmax,int *dmax_tag,Point point[],int left,int right)
{
    *dmax=-1;//初始化个小值
    int i;
    double distance;
    double k=(point[left].y-point[right].y)/(point[left].x-point[right].x);//不考虑斜率不存在的无聊情况
    double b=point[left].y-k*point[left].x;
    //点到直线距离公式：(k*x-y+b)/√(k*k+1)
    for(i=left+1;i<=right-1;i++)
    {
        distance=fabs((k*point[i].x-point[i].y+b)/sqrt((k*k+1)));
        if(distance>=*dmax)
        {
            *dmax=distance;
            *dmax_tag=i;
        }
    }
}

///道格拉斯——普克法算法
void fun(Point point[],int left,int right,double Dis)
{
    if(left>=right-1)///少于三个点就退出了
    {
        return;
    }
    else
    {
        double dmax;//最大高度
        int dmax_tag,i;//最大高度对应的点号
        getmax(&dmax,&dmax_tag,point,left,right);//把dmax,dmax_tag指针传进去为了返回来
        if(dmax<Dis)//舍去
        {
            for(i=left+1;i<=right-1;i++)
            {
                point[i].tag=0;//置舍去了的以0标记
            }
        }
        else
        {
            ///递归，并以dmax_tag点为界，把曲线分为两部分，对这两部分重复使用该方法
            fun(point,left,dmax_tag-1,Dis);
            fun(point,dmax_tag+1,right,Dis);
        }
    }
}

转载自：https://blog.csdn.net/weixin_42034217/article/details/84800623