三调专题（一）宗地四至提取的量化算法及FME实现

作者：凡江林   QQ：564438737

专题背景

2017年10月16日，国务院印发《关于开展第三次全国土地调查的通知》（国发〔2017〕48号）

2017年12月12日，贵州省人民政府印发《关于开展贵州省第三次全国土地调查的通知》（黔府发〔2017〕33号）

……

2018年6月23日，贵州省土地学会印发《关于举办贵州省第三次全国土地调查专业技术培训班的通知》（黔土学发〔2018〕12号）

问题描述

宗地四至提取的最初需求，源于几年前“ArcGIS+Python+FME学习交流”群和“FME中国技术交流”群中，群成员的提问。主要是关于“农村土地承包经营权确权登记”中，需要填写宗地的四至。

在2018年（7月1日）—（7月4日）参加的“贵州省第三次全国土地调查专业技术培训班”中，土地利用数据库标准中的“宗地属性结构”表中，也涉及到宗地四至的提取。

通过研究目前的四至算法发现。这些方法有一个共性，都是把一个地块作为一个整体，通过设置相关的参考点，或是参考线；进而划分四至线角度或是求取四至线。通过四至线来求取宗地的四至。自始至终的关注点都在某一个宗地以及对应的四至线或四至区域的划分。在综合这些算法后发现，这些算法都存在一个局限性，就是对于某一类规则的或是与规则符合的效果较好，但是对于其他的情况实用性不佳。具体的相关算法或是相关改进的算法，可以参考相关的论文或是博文资料，在此不再详述。

本文要解决的问题之一是从量化的角度考量宗地四至的定义；问题之二是以FME作为工具，来实现宗地四至的量化算法。

宗地四至的量化定义

在百度百科中，宗地四至的定义为：“宗地四至是指一宗地四个方位与相邻土地的交接界线。一个地块内由几个土地使用者共同使用而其间又难以划清权属界线的也称为一宗地。一般填写四邻的土地所有者或使用单位和个人的名称。”如图（1）所示。

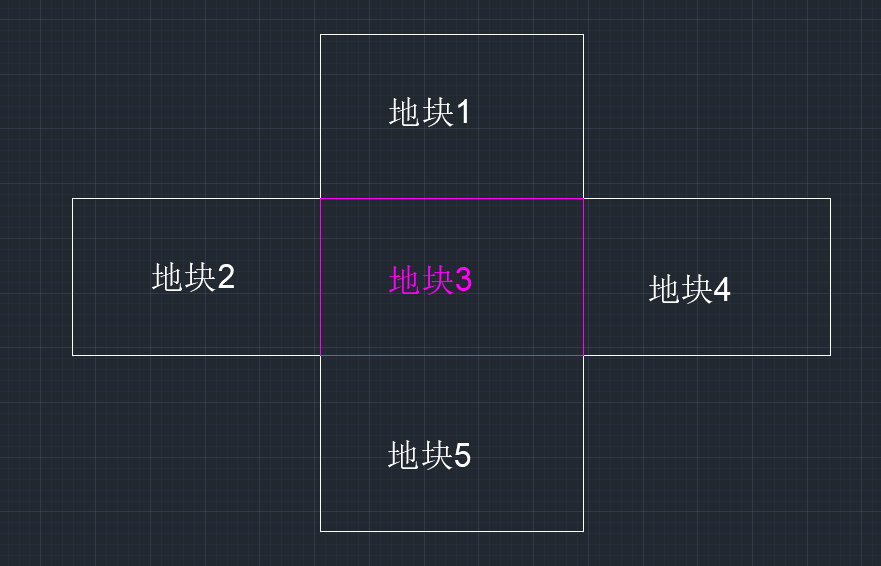
                                                                                              图（1）

 

 

在图（1）中，地块3的北至为：地块1；东至为地块4；南至为：地块5；西至为：地块2。这是最符合定义的情况。现在，我们对以上的情况进行演变。如图（2）所示。

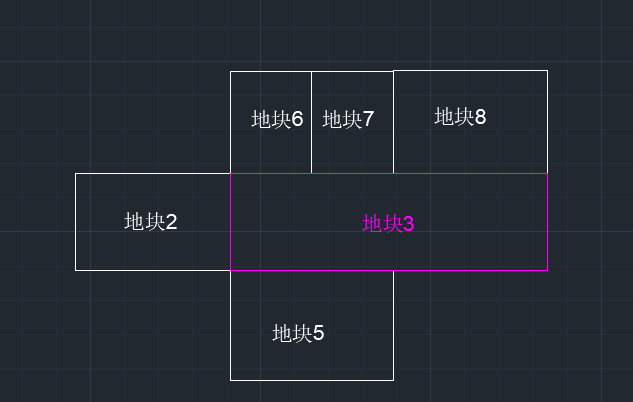
                                                                                                  图（2）

 

在图（2）中，地块3的北至为：地块6、地块7、地块8。进一步演变。如图（3）所示。

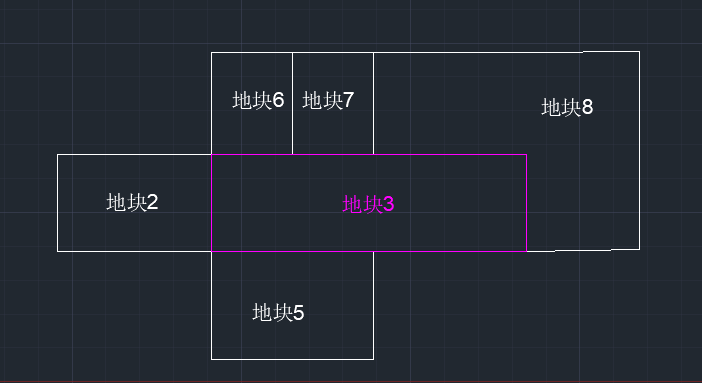
                                                                                             图（3）

 

在图（3）中，地块3的北至为：地块6、地块7、地块8；东至为：地块8。进一步演化。对于一般的情形，如图（4）所示。

 

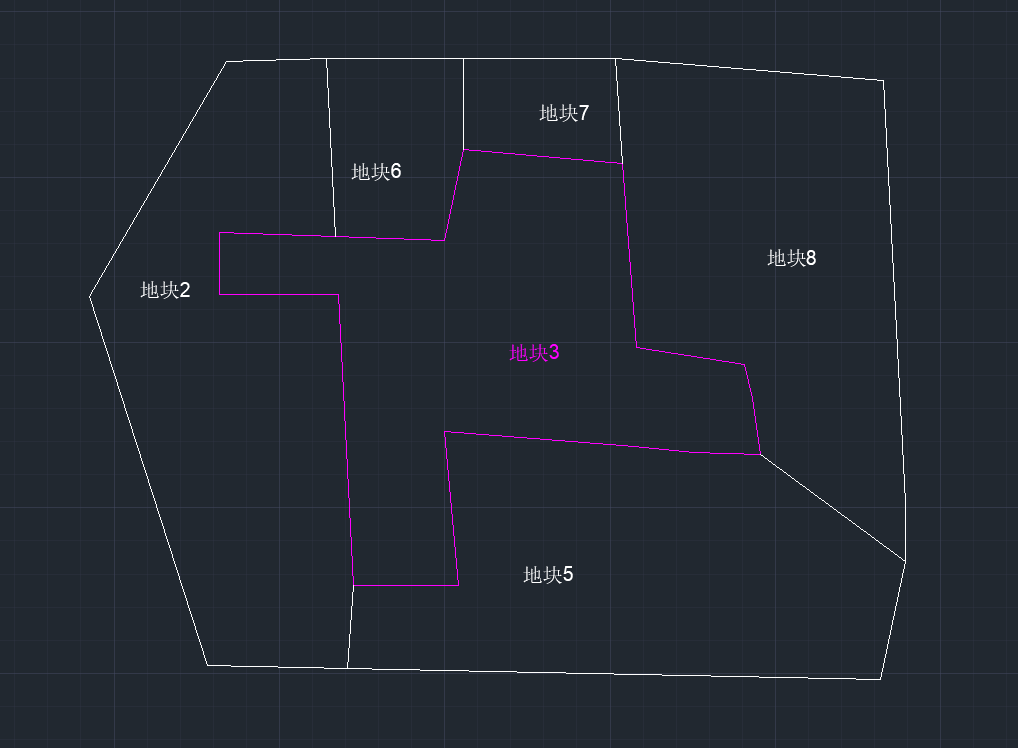
                                                                                             图（4）

 

在图（4）中，地块3的北至为：地块2、地块6、地块7、地块8；东至为：地块8、地块5；南至为：地块5、地块2；西至为：地块6、地块2。这个图值得研究。原因在于，从这个图中，我们能够隐约感觉到如果四至用四至线来度量的话，那么，四至线经常是不连续的。如图（5）所示。

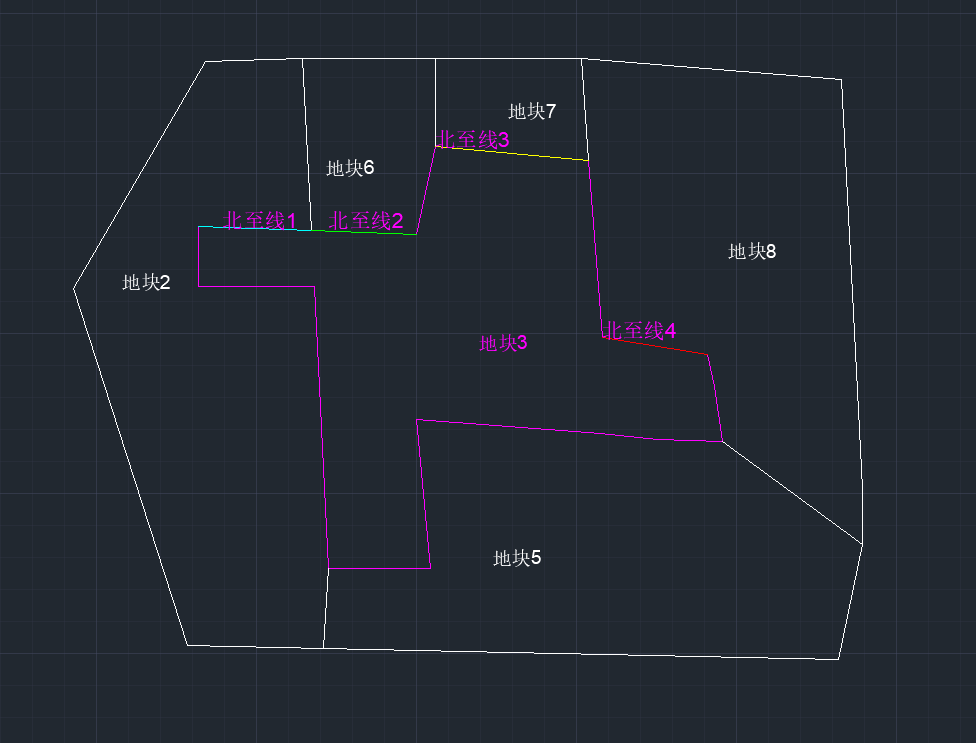
                                                                                               图（5）

 

在图（5）中，用不同的颜色及文本注记标识了北至线1、北至线2、北至线3、北至线4。基于此种思路。我们可以进一步探索。从逻辑上，对一个宗地对应的边界线进行分解。分解到每一条线段。是的，没错，就是分解到每一条线段。我们从线段的角度进行考量。

从宗地边界的每一条边界线段进行考量后，我们发现，四至定义的思路拓展开了。对于不规则的宗地，如果是通过参考点或是参考线，硬生生的把边界分为东西南北四段显然是简单粗暴的。如果是对每一条边界线段进行考量，判断是东西至线，或是南北至线的话，得到的结论也是令人惊奇的。通过这样的方式，我们把宗地四至的定义量化了。

宗地四至的量化定义

对于任意一块宗地，我们把宗地的边界线分解为一段一段的线段。我们把边界线段分为北至线段、东至线段、南至线段、西至线段。其中，北至定义为：所有北至线段临接（或是带缓冲区临接）的宗地；东至定义为：所有东至线段临接（或是带缓冲区临接）的宗地；南至定义为：所有南至线段临接（或是带缓冲区临接）的宗地；西至定义为：所有西至线段临接（或是带缓冲区）临接得宗地。

在具体实现过程中，会发现两个地块A、地块B临接的一段公共线段L。公共线段L对于地块A来说是北至线段，那么对于B来就是南至线段。反之亦然。如图（6）所示。

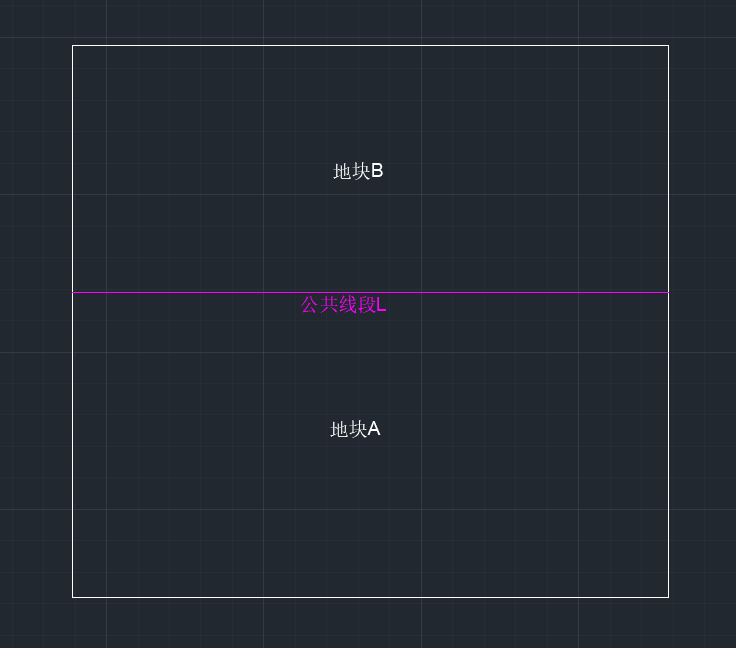
                                                                                               图（6）

 

宗地四至的量化算法及FME实现

在完成了宗地四至的量化定义以后，现在来探讨宗地四至的量化算法。

算法的大致思路如下：

输入宗地面  =>  分解宗地面为不重复的线段（过滤掉0长度的线段，以及）=>  过滤重叠线及长度限值以下的线段 =>  编号 =>  线段中垂线两端点四至属性提取 =>  带四至属性的中垂线的端点与最开始的输入宗地面空间叠加，获取四至属性。=>  整理宗地四至属性，输出宗地四至。相关的FME流程图，如图（7）所示。其中，用到了自定义转换器，以及高中数学及解析几何中的相关知识。在此不再详述。

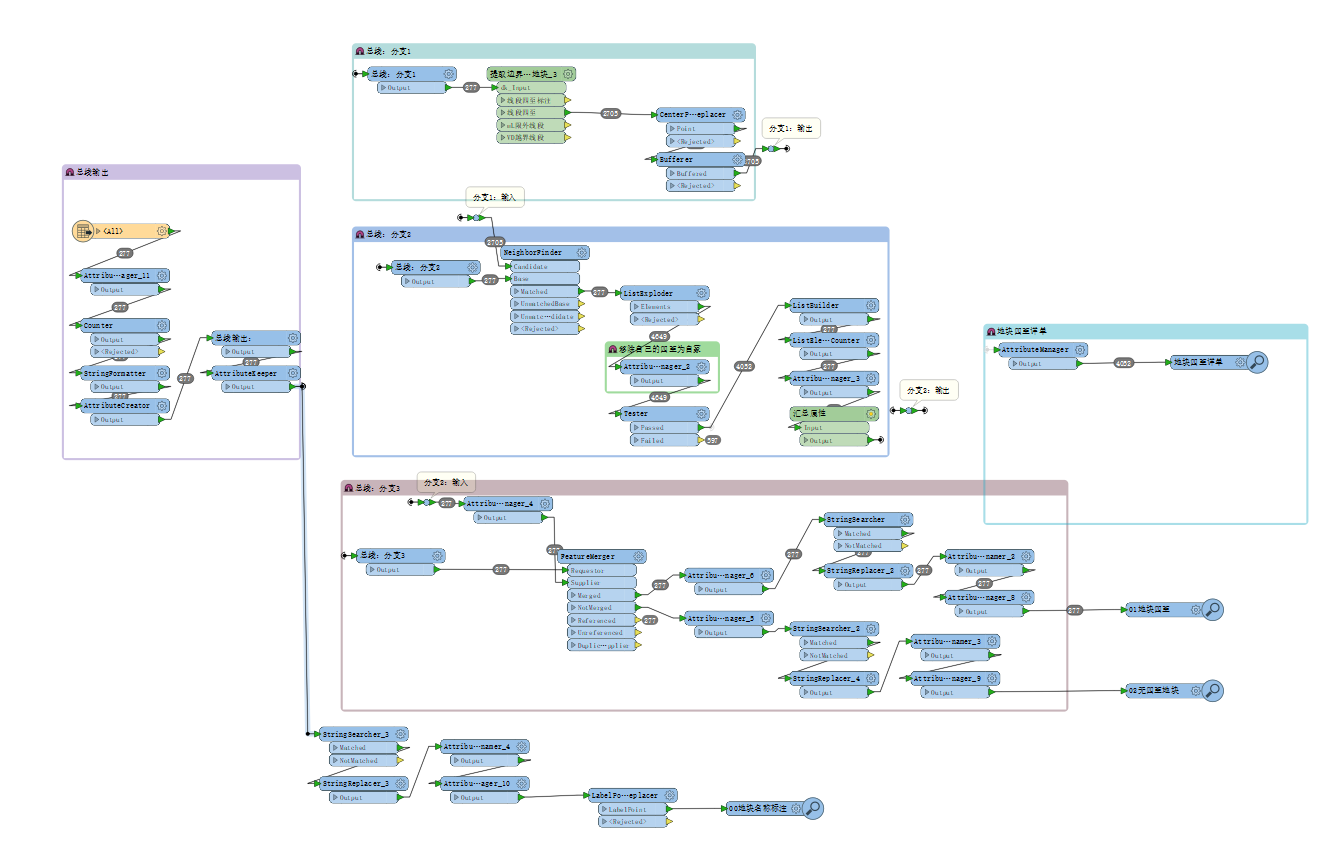
                                                                                             图（7）

 

 

基于工作中一份地块数据运行，对应的成果如图（8）所示。

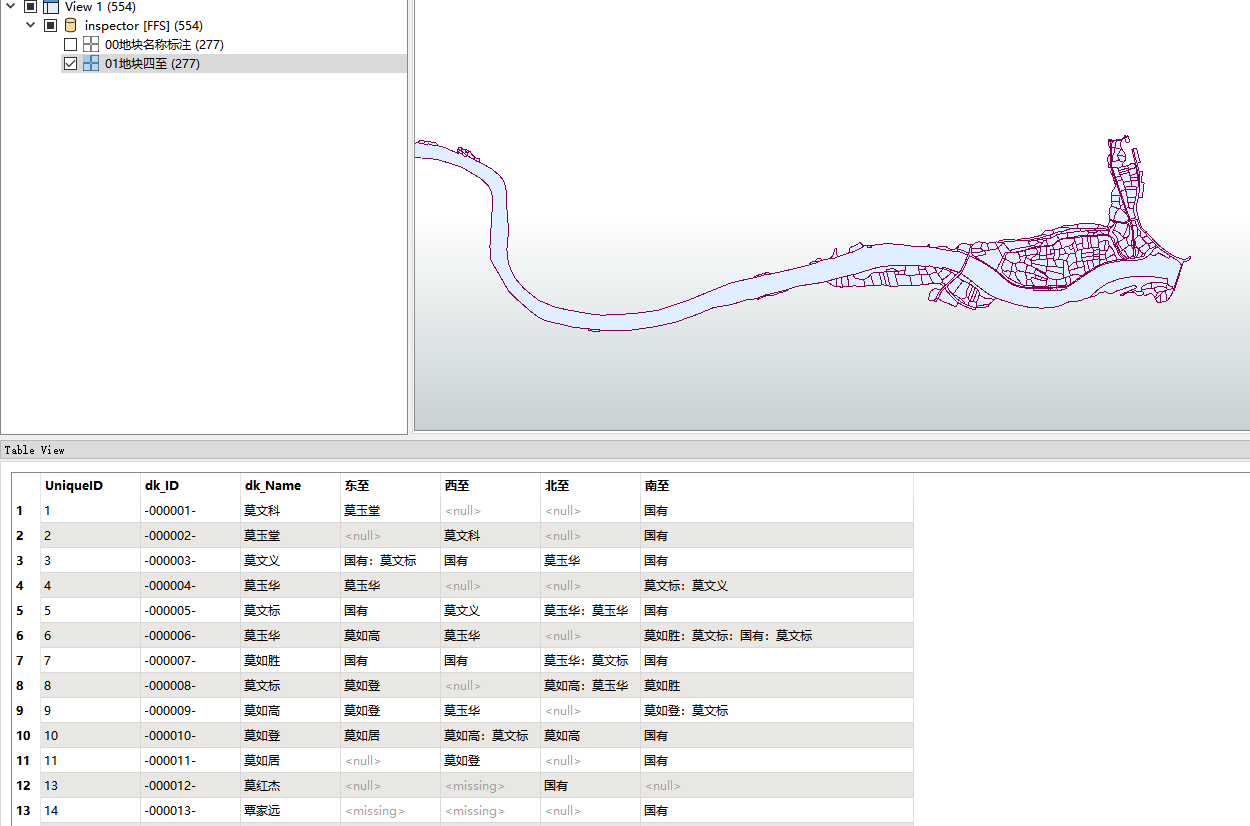
                                                                                         图（8）

 

 

 

 探索结论

至此，完成了宗地四至量化定义详解及量化算法思路的讲解。上文中的FME实现是两年前的实现，现在对于细节已经有些模糊。不过，最重要的是宗地四至的量化定义及量化算法的思路，基于此，可以选择不同的实现方式。并且，在完成了上述FME实现后的一段时间，感觉自己的实现版本可以进一步优化改进，从而到达更接近真实情况的四至结果。也发现在实际工作中，可以加入更多的限制因素，比如根据项目的需要，限制线段的长度以及四至线段角度的范围。如果读者考虑也用FME来实现，可以考虑利用图（9）所示的转换器来简化部分工作。但如果涉及到跨缓冲区的情形，依然需要利用解析几何中相关的概念及知识。当然，想象有多大，世界就有多大。宗地四至提取的量化算法也可以更进一步开拓与创新。期待读者也能够分享你们的算法与思路。相互交流，共同进步。

                                                                                                图（9）

 

 

（限于作者的学识和经验，定有不少疏漏和不当之处，甚至是错误也在所难免，恳请读者和同行批准指正！）

转载自：https://blog.csdn.net/fanjianglin/article/details/81087498