通过C#代码实现空间离散点的克里金(kriging)插值
目录
转自:https://blog.csdn.net/zhangkechun/article/details/50471724
说明:克里金插值较为复杂,但效果也是比较好的。为了能够通过代码实现克里金插值的过程,首先需要了解其详细的计算过程。先在ArcGIS中操作一遍并查看帮助文档详细了解其算法
参见:https://blog.csdn.net/zhangkechun/article/details/50438025
程序下载
本文的程序下载:克里金插值及DEM等高线生成
回顾算法流程
- 求取已知点的距离以及点对的半方差
- 筛选第一步求取的结果,计算出几个均值点,用于拟合
- 选定拟合模型,为了方便代码实现,我选择了指数模型
- 用指数模型去拟合第二步得出的均值点,得出偏基台值 c” role=”presentation” style=”position: relative;”>cc
- 根据拟合得到的模型,按照公式通过已知点高程计算位置点高程
通过C#实现的难点
在试图实现这个算法的过程中,首先碰到的难题是算法不懂,但是这个问题已经解决了。接下来的难题是,如何用C#进行离散点的拟合,以及如何高效的实现算法中公式的矩阵运算。
为了解决以上的问题,我利用了网络上的C#的数学库,比较好的有:开源的“Math.NET”,以及收费的“ILNumerics”,我选用了“Math.NET”,官网:Math.NET
如何将Math.NET加入到自己的项目中:
参考网页:Math.NET Numerics
在VS的主界面上,选择“工具”=>“NuGet程序包管理器”=>“程序包管理器控制台”,可以看到这样的界面:
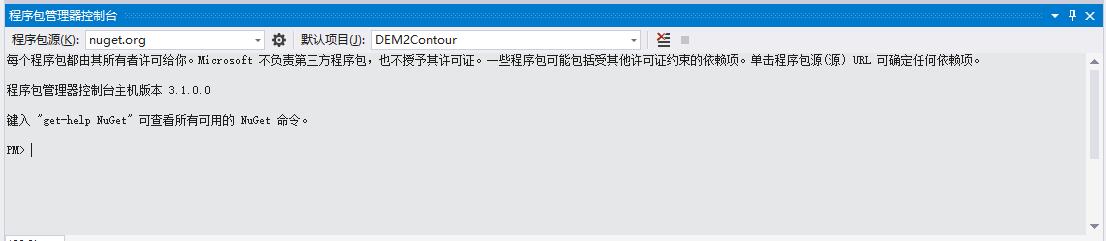
输入“Install-Package MathNet.Numerics”后,回车,等待片刻即可。
算法实现
1,求取已知点的距离以及点对的半方差
点对的半方差计算公式:
Semivariogram(distanceh)=12∗(valuei–valuej)2” role=”presentation” style=”position: relative;”>Semivariogram(distanceh)=12∗(valuei–valuej)2Semivariogram(distanceh)=12∗(valuei–valuej)2
计算结果为一堆横坐标为distanceh” role=”presentation” style=”position: relative;”>distancehdistanceh的点。
将这些点按照横坐标分为约10份,(此处可按照实际情况修改),计算每个区间里的点的横坐标纵坐标均值,这样就能得到10个点代表刚刚的整个计算结果。
如果点数过多,拟合的效果以及效率会受到影响。
2,拟合刚刚计算得到的点
拟合的方法我参考了网站使用Math.NET求解线性和非线性最小二乘问题,这篇文章翻译自Linear And Nonlinear Least-Squares With Math.NET,网页最后给出了示例代码,下载地址:article-least-squares-source.zip
我提取了其中的高斯牛顿法实现的拟合算法,主要由“GaussNewtonSolver”类和“PowerModel”类组成,读者也可以试着使用示例代码所提供的别的拟合算法来完成。
拟合的过程比较复杂,我自己也不是很懂,读者可以去细读上面提供的文章。
下图是我的DEM:
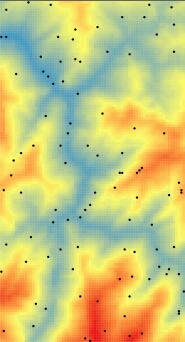
我在已知的DEM上选取随机点,再利用这些随机点进行插值,方便比较计算结果与原始值。
下图是这些随机点的半方差拟合结果:
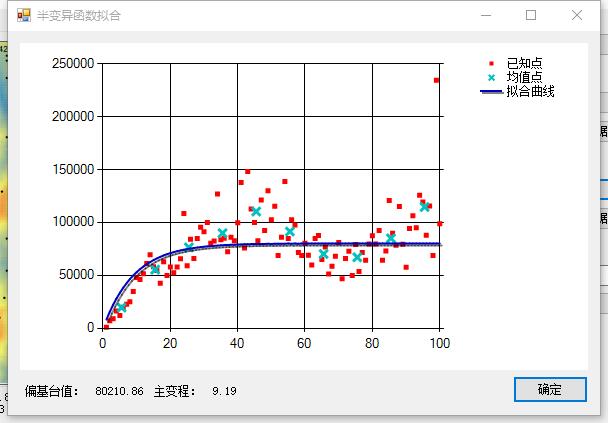
红色的点是初始计算的结果,实际上已经做过一次筛选了,因为选取的随机点约100个,初步计算出来的半方差值约有9900个。蓝色的叉叉是再次筛选后的结果,每隔10个单位的区间计算一个平均点。深蓝色的线即为对蓝色叉叉的拟合。
实际上,我用同样的离散点在ArcGIS中做一次插值,我的拟合结果与ArcGIS的拟合结果有一定差距,偏基台值基本一致,主变程值只有ArcGIS的拟合结果的一半,如果追求准确的插值结果,需要考虑对拟合算法的优化。
3,根据拟合模型计算未知点高程
以下提到的数学参数请对照《计算原理》一文中的定义。
定义方法:
private double CalCij(double x1, double y1, double x2, double y2)
{
double distance = Math.Sqrt(
Math.Pow(x1 - x2, 2) + Math.Pow(y1 - y2, 2));
if (distance == 0)
{
return formula_c;
}
else
{
return formula_c* Math.Exp(-distance / formula_r);
}
}- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
计算两点之间的Cij” role=”presentation” style=”position: relative;”>CijCij 就是模型结果中的一个值。
计算矩阵 K” role=”presentation” style=”position: relative;”>KK:
//size为已知点的个数
var K = new DenseMatrix(size, size);
for (int m = 0; m < size; m++)
for (int n = 0; n < size; n++)
K[m, n] = CalCij(
pointList[m].X,
pointList[m].Y,
pointList[n].X,
pointList[n].Y);- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
计算矩阵 K” role=”presentation” style=”position: relative;”>KK:
Kn = K.Inverse();- 1
假设求坐标为 (m,n)” role=”presentation” style=”position: relative;”>(m,n)(m,n) 的未知点的高程:
1. 计算向量 D” role=”presentation” style=”position: relative;”>DD:
var D = new DenseVector(size);
for (int p = 0; p < size; p++)
D[p] = CalCij(randomPointList[p].point.X,
randomPointList[p].point.Y, m, n);- 1
- 2
- 3
- 4
- 计算λ(i)” role=”presentation” style=”position: relative;”>λ(i)λ(i) 个已知点对当前未知点的影响权重:
var namuta = Kn.LeftMultiply(D);- 1
- 计算 Z(xi)” role=”presentation” style=”position: relative;”>Z(xi)Z(xi) 个点的高程值:
for (int q = 0; q < size; q++)
interpolationDEMData[m, n] +=
namuta[q] * randomPointList[q].altitudeValue;- 1
- 2
- 3
至此,坐标为 (m,n)” role=”presentation” style=”position: relative;”>(m,n)(m,n) 数组中。
下图为插值结果:
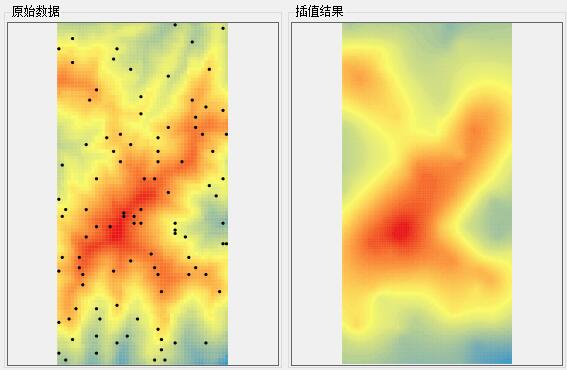
结果与原始数据相比较,还是比较准确的。
转载自:https://blog.csdn.net/liujianxun111/article/details/79891748