GIS中最短路径分析——Dijkstra算法
目录
GIS中最短路径分析——Dijkstra算法
一、算法思想:
网络分析是GIS一重要的分析类型。在地里空间中,许多自然、人工的线状第五相互间构成网络。
最短路径分析方法如下:
在最短路径选择中,两点之间的距离可以定义为实际距离,也可以定位为两点间的时间、运费、流量等。换句话说,可以定义为使用这条边的代价。因此,可以对不同的专题进行最短路径分析。下面介绍的最短路径搜索算法是迪克斯特拉(Dijkstra)在1959年提出的,被公认为是最好的算法之一。它的基本思想是:把图的一页顶点分为S、T两类,若起始点 u 到某顶点 x 的最短通路已求出,则将 x 归入S,其余归入T,开始时S中只有
u ,随着程序运行,T的元素逐个转入S,直到目标顶点 v 转入后结束。
u ,随着程序运行,T的元素逐个转入S,直到目标顶点 v 转入后结束。
二、数据结构
为了描述网络我们采用图的数据结构,并用邻接矩阵对其进行存储组织。如下图:

注:该图为有向图,定义A->B的距离为4,B->A的距离为无穷大。
三、最短路径搜索的依据
网络图中的最短路径应该是一条简单路径,即使一条不与自身相交的路径。
最短路径搜索的基本依据是,若从S到点T有一条最短路径,则该路径上的任何点到S的距离都是最短的。证明从略。
四、算法流程
初始状态
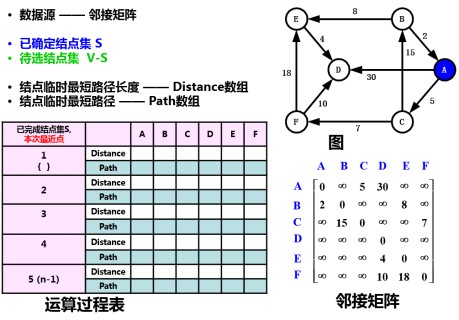
将点A加入S集合,计算S集合到T集合中各点(B、C、D、E、F)的距离,找到最邻近点C
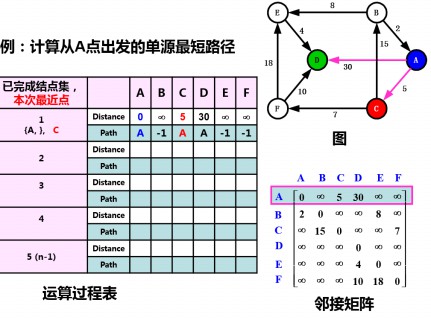
将点C加入S集合,计算S集合到T集合中各点(B、D、E、F)的距离,找到最邻近点F
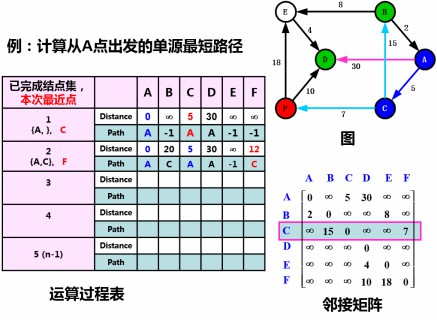
将点F加入S集合,计算S集合到T集合中各点(B、D、E)的距离,找到最邻近点B
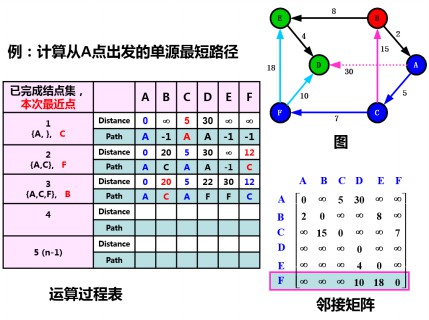
将点B加入S集合,计算S集合到T集合中各点(D、E)的距离,找到最邻近点D

将点D加入S集合,计算S集合到T集合中点E的距离

最终,通过对Path数组反向搜索得到最短路径,如D结点相对于A的最短路径为:D->F->C->A
五、代码
我们采用递归的思想遍历图(无向图)中各结点,每次迭代的过程中首先依据输入参数对Path数组进行更新,
再遍历新的Path数组,计算下一次迭代的参数(本次最邻近点以及S中点的距离)。
算法核心代码如下:
/**
* @brief
* @param1 路径搜索的起点 A-0
* @param2 存储邻接矩阵和顶点数组的图结构
* @param3 图中顶点数
* @param4 指向路径起始位置的指针
* @param4 指向路径结尾后的指针
* @return
*/
template<class T,class E>
void Dijkstra(int v,Graphmtx<T,E>& graphmtx,int times,MinPath<T,E>* ptrBegin,MinPath<T,E>* ptrEnd,E dis)
{
int nextVertex=v;
int j=0;
for(MinPath<T,E>* it=ptrBegin;it!=ptrEnd;it++){
if(dis+graphmtx.getWeight(v,j)<it->Distance){
it->Distance=dis+graphmtx.getWeight(v,j);
it->path=graphmtx.getValue(v);
}
j++;
}
E currentDis=maxValue;
int k=0;
for(MinPath<T,E>* it=ptrBegin;it!=ptrEnd;it++){
T ele=graphmtx.getValue(k);
if(it->Distance<currentDis&¬Include(ele,ptrBegin,ptrEnd)){
currentDis=it->Distance;
nextVertex=k;
}
k++;
}
if(times--!=1){
Dijkstra(nextVertex,graphmtx,times,ptrBegin,ptrEnd,currentDis);
}
}涉及的数据结构:
template<class T,class E>
class Graphmtx:public Graph<T,E>{
friend istream& operator>>(istream& in,Graphmtx<T,E>& G);
friend ostream& operator<<(ostream& out,Graphmtx<T,E>& G);
public:
Graphmtx(int sz);
~Graphmtx(){
delete []VerticesList;
delete []Edge;
}
T getValue(int i){
return i>=0&&i<numVertices?VerticesList[i]:NULL; // 返回顶点数组总的第i个元素 [8/26/2014 pan]
}
E getWeight(int v1,int v2){
return (v1!=-1&&v2!=-1) ? Edge[v1][v2] : 0; // 返回该边的路径代价 [8/26/2014 pan]
}
int getFirstNeighbor(int v);
int getNextNeighbor(int v,int w);
int NumberOfVertices(){return numVertices;}
bool insertVertex(const T& vertex);
bool insertEdge(int v1,int v2,E cost);
bool removeVertex(int v);
bool removeEdge(int v1,int v2);
public:
T * VerticesList; // 顶点表 [8/25/2014 pan]
E ** Edge; // 邻接矩阵 [8/25/2014 pan]
int getVertexPos(T vertex){
for(int i=0;i<numVertices;i++){
if(VerticesList[i]==vertex){
return i;
}
return -1;
}
}
int maxVertices;
int numEdges;
int numVertices;
};template<class T,class E>
class MinPath{
public:
E Distance; // 当前最短距离 [8/26/2014 pan]
T path; // 上一个节点 [8/26/2014 pan]
public:
MinPath(){this->Distance=maxValue;}
~MinPath(){}
};这里要说明一下,所有的MinPath对象一定要利用默认的构造函数将其Diatance属性赋值为maxValue,
否则会导致算法错误。
template<class T,class E>
bool notInclude(T ele,MinPath<T,E>* ptrBegin,MinPath<T,E>* ptrEnd)
{
for(MinPath<T,E>* it=ptrBegin;it!=ptrEnd;it++){
if(it->path==ele){
return false;
}
}
return true;
}图与Path数组的初始化(写的很拙计不要笑话):
Graphmtx<char,int> graphmtx(6);
char points[6]={'A','B','C','D','E','F'}; //0 1 2 3 4 5
graphmtx.VerticesList=points;
int list1[6]={0,2,5,30,maxValue,maxValue};
int list2[6]={2,0,15,maxValue,8,maxValue};
int list3[6]={5,15,0,maxValue,maxValue,7};
int list4[6]={30,maxValue,maxValue,0,4,10};
int list5[6]={maxValue,8,maxValue,4,18};
int list6[6]={maxValue,maxValue,7,10,18,0};
for(int i=0;i<6;i++){
graphmtx.insertEdge(0,i,list1[i]);
graphmtx.insertEdge(1,i,list2[i]);
graphmtx.insertEdge(2,i,list3[i]);
graphmtx.insertEdge(3,i,list4[i]);
graphmtx.insertEdge(4,i,list5[i]);
graphmtx.insertEdge(5,i,list6[i]);
}
MinPath<char,int> *minPath=new MinPath<char,int>[6]();
MinPath<char,int> *ptrBegin=minPath;
MinPath<char,int> *ptrEnd=minPath+6;最后贴一张gif图,来看一下递归过程中数据在内存中的变化:

转载自:https://blog.csdn.net/panan160/article/details/38842523