白话空间统计二十四：地理加权回归（五）

这是写概念的最后一节……从下一节开始，大家就可以告别枯燥的理论和概念了（此处应有掌声）

上一章节写到，地理加权中，空间关系的比广义的空间关系的限制要多得多，常用的就是用距离衰减的方法，而这种方法最常见的又是高斯函数以及扩展高斯函数方法，最后埋下了一个坑，高斯函数相关的算法，最重要的一个选择，就是带宽的定义。

讲到带宽这个词，实际上如果一直跟的同学，应该很熟悉了，我在《白话空间统计第二十一：密度分析》的第四节和第五节，对带宽的概念和意义，有过详细的阐述，不记得了的同学，或者没有看过的同学，可以访问以下文章：

白话空间统计第二十一：密度分析（四）

白话空间统计第二十一：密度分析（五）

实际上，所谓的带宽，通常就是一个影响的范围，从我上面两篇文章给出的所有例子，大家都会发现，实际上对各种函数的选择，都不那么敏感，但是对带宽的选择，确相当的敏感。可是如何选择最佳带宽，就实在是不好进行量化了，包括在密度分析里面，很多时候都用的是经验公式（或者说是视觉感来判定的），所幸的是，地理加权回归里面，提出了几个理论以及相应的指数来对“最佳”带宽，进行探索和应用。

首先第一个方法，就是最经典，也最常用的“交叉验证法”（Cross Validation)。其实在地理加权回归（三）的时候，简单讲过CV方法，但是不够详细，下面详细描述一下这个有着广泛应用的一种方法。

先还是进入历史科普时间：

最早提出CV方法的是美国普渡大学（purdue university）的计算机科学系教授William Swain Cleveland II （威廉 斯万 克利夫兰二世：下图那个老帅哥）在1979年提出的，开始提出来的时候，主要用来进行局部回归的验证，后来到处开花，成为了最优参数探索过程中的使用最广泛的方法。

普渡大学是我国两弹一星元勋邓稼先的母校，也是全美第一个开设计算机科学系的大学，属于全球理工类院校的扛把子之一。克利夫兰教授在耶鲁大学获得统计学博士之后，在贝尔实验室统计学研究部门工作和当然领导长达12年之久，后来加入普渡大学计算机系教授统计学和计算机科学，是全美顶级的计算机学家和统计学家。

交叉验证法的思想其实非常的简单，说起来就是分组轮流坐庄……可以参考美国大选——民主党上台执政，共和党负责在台下找茬监督；下一期，共和党上台执政了，民主党开始负责找茬 监督。

这种方法通俗的说起来，就是把数据分成N组，使用其中一部分用来计算，另外一部分数据就用来验证；之后用另一部分进行计算，使用前一部分进行验证。如下图所示的，用来验证几种战术优劣的方法：

如果要验证哪种战术效果最后，最简单的方法就是把所有队员分成若干组，然后用不同的战术相互进行PK，PK完了之后，重新随机分组（不断随机分组，是为了避免某个（些）队员个人能力超强这种情况），最后统计不同战术的胜率，优劣就自然出来了。这种方法就是交叉验证法的一种具体应用。

CV的公式如下所示：

其中，

表示在回归参数估计的时候，不包括回归点本身，只根据回归点周边的数据进行回归参数计算，然后把不同的带宽和不同的CV绘制成趋势线，那么就可以找出CV值最小的时候，对应的最佳带宽是多少了。

第二种方法，就是所谓的AIC法，（Akaike information criterion、简称AIC，有时候也叫“最小信息准则”或者“赤池信息量准则”，是衡量统计模型拟合优良性的一种标准，是由日本统计学家赤池弘次创立和发展的），历史科普内容，请参考地理加权回归（三）。

AIC法的公式如下：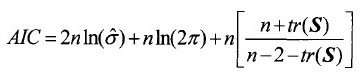

好吧，我知道这个公式很复杂……那么下面我们用最通俗的话来说说这个AIC法的原理是啥：

简单的说，就是用两个参数来对模型进行估计：

AIC = （2倍（模型的独立参数个数）- 两倍 ln(模型的极大似然函数））/ 观测值个数

ln是自然对数函数。

首先AIC法假设误差的出现是服从独立正态分布的，所以采用极大似然函数就有意义了。（极大似然函数的问题，请大家自信百度……简单的说，就是一种建立在统计分布上的估算方法，假设有N种结果，如果我们仅作一次实验，出现哪个结果，就认为哪个结果概率最大，这种简单粗暴的方法，我喜欢。）

这样这个方法就好理解了，当我们有一堆可供选择的模型参数的时候，选择AIC最小的那个就行……因为AIC的大小取决于独立参数的个数和模型的极大似然函数两个值，参数值少，AIC小，且极大似然函数大，AIC也小，参数少表示模型简洁，极大似然函数大表示模型精确。因此AIC和修正的决定系数类似，在评价模型是兼顾了简洁性和精确性

当两个模型之间存在较大差异的时候，这个差异肯定首先出现在模型的极大似然函数上；而这个函数没有出现显著的差异的时候，模型的独立参数个数才气作用了，从而，参数个数越少的模型，表现得越好。也就是这个原因，这个准则才被称为：最小信息准则。

AIC法认为加入自由参数，可以提高拟合度（废话，自由参数多了，不就非线性了么）……但是AIC鼓励数据拟合的优良性但是尽量避免出现过度拟合。

到此为止，地理加权回归的所有概念，也就介绍完了，从下一章开始，进入实际操作环节，用ArcGIS和R语言等工具，来具体看看如何使用地理加权回归来解决实际分析过程。

待续未完

转载自：https://blog.csdn.net/allenlu2008/article/details/69388540