白话空间统计十六:增量空间自相关
遇上瓶颈……所以进来更新稍微有点慢了……大家见谅
点数据的密度计算,是一个很常用的分析方式,在计算密度的时候,最令人头痛的是如何去确定密度的距离,也就是密度收集区域的半径,那么从这句话看,也就知道我们这篇文章是干嘛的了。

距离,又见距离!
不同的情况下,分析空间数据对使用的距离是非常敏感的。对于不同的分析,使用的距离也是不同的。比如你要计算人的活动区域热点,步行的话,一般不会超过3公里,而骑自行车,就变成了5-10公里了。
所以在做类似热点分析或者密度分析的时候,选择一个合适的距离,非常重要的事情。
那么怎么选择一个合适的距离的?如果你以前这样问虾神,虾神我会告诉你一个虾神的独门绝技,那就是——瞎猜……

好吧……既然虾神的绝技被破,我们只能用这个所谓的“增量空间自相关”来对距离进行探索了。
首先从名称上看,这个神奇的工具首先是用来计算空间自相关的,有关空间自相关的解释,请参考白话空间统计的第一话,讲的就是这个空间统计学里面的理论基础概念。
当然,空间相关性涉及到各种指数,比如莫兰指数、P值、Z得分神马的,大家有兴趣的话去翻以前的文章(知道什么叫万丈高楼平地起了吧……基础概念不过关,后面就只能看图看热闹了。)
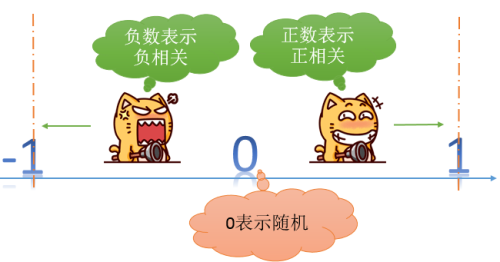
好吧,我知道有的同学记不住了,这里来复习一下,通常来说,莫兰指数是一个有理数,经过方差归一化之后,它的值会被归一化到–1.0——1.0之间。如下图:
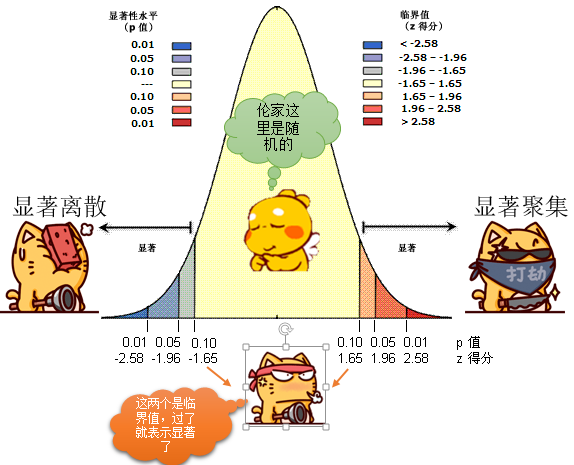
然后自然要看聚类或者离散的程度了,老规矩,Z得分出马,Z得分的概念,详细的说明也请去翻历史消息,这里来一张图片简单的复习一下:
基础内容复习完了,下面进入具体的算法说明:
这个算法其实与上一篇文章讲的多距离空间聚类方法很像,就是通过不同的距离进行迭代计算,然后对计算出来的值进行比较,最后给出迭代计算结果的建议。
过程与多距离聚类计算很像,但是也有不同的地方。首先是在上一个方法计算的是,可以忽略每个点上面的属性值(当然你可以设定权重来进行计算),但是在增量空间自相关上面,对要素的属性数据是一定需要的,否则你就没办法确定是否是随机结果了。对比如下:
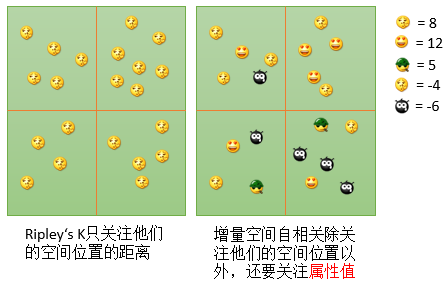
所以,如果你的数据分析,只关心空间位置,那么实际上没必要使用这个工具,用多距离聚类分析就行了,但是如果你关注的除了空间位置以外,还需要关心数据属性的话,就有必要采用这个工具了。另外需要说明的是,参与计算的属性值,一般是数字类型的值。
看下面这个例子:
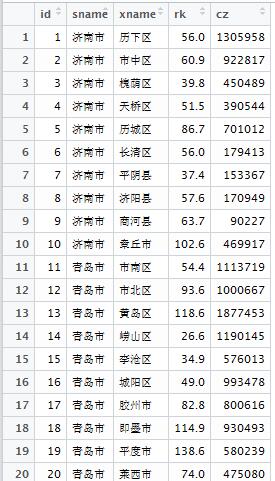
我们手上有一份上海市停车场的数据,大约有2900多条,数据描述如下:
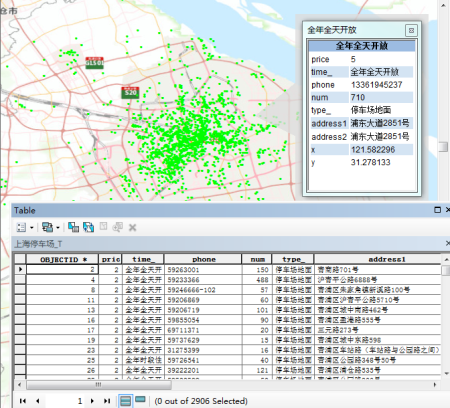
我们现在要研究他们的空间分布热点以及聚集度情况,并且以价格price字段作为他们的聚类属性约束,从空间上和价格上进行聚类研究。
最简单的方法就是做一个核密度计算,以价格为高斯核函数的自变量带入进行计算,如下:
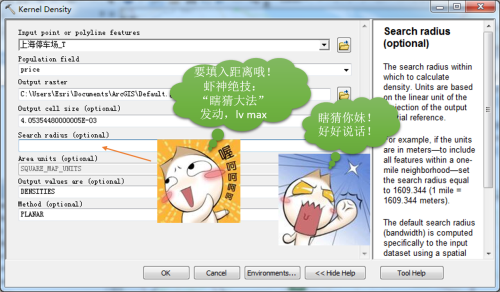
好吧,既然瞎猜大法已经失效了,就启动增量空间自相关工具算算好了,工具说明如下:
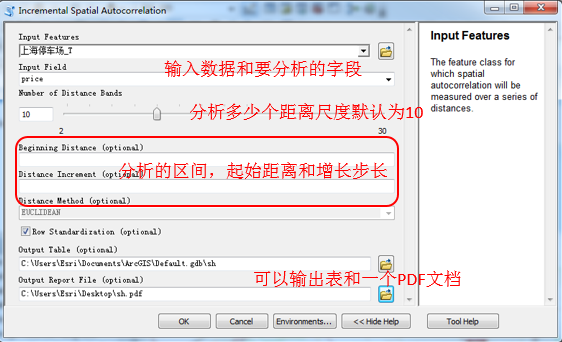
需要注意的是分析的区间,这个区间值如果不手动设置数据的话,系统会直接采用最小距离来计算,这样如果你的数据有一些明显的离群点的话,就会出现非常郁闷的结果。
我们先采用完全默认的参数,计算结果如下:
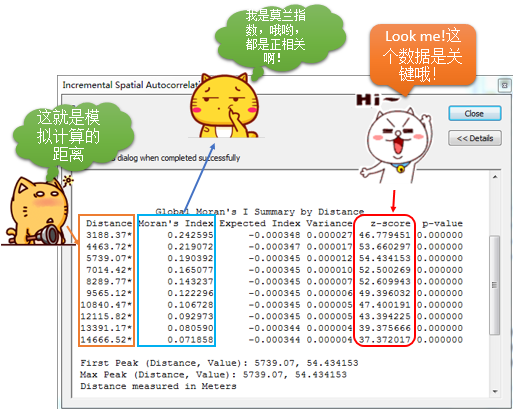
如果你选择了生成pdf,还会生成一个PDF,内容如下:
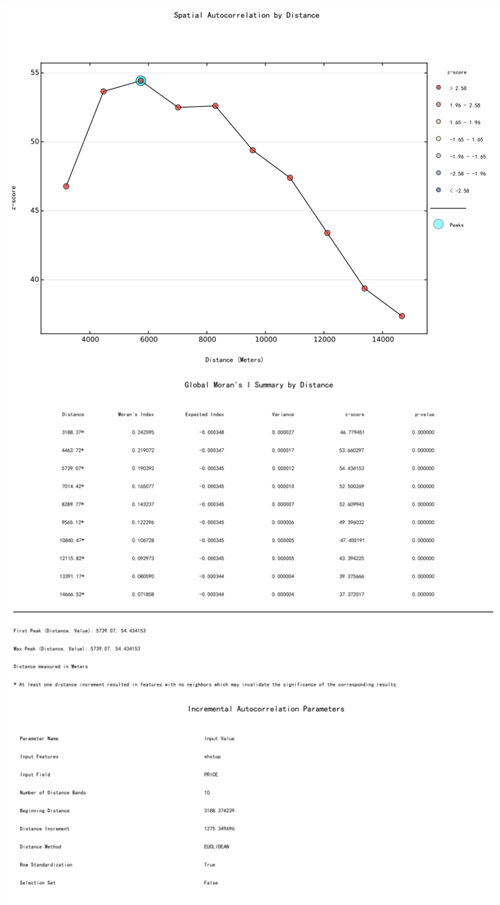
主要是把上面的内容通过统计图表的方式展现出来。
其中我们可以看见,有一个点,被特别加亮的标识了出来,这个就是系统计算出来的,认为这个峰值反映这份数据促进空间过程聚类最明显的距离是多少。
那么下面通过计算出来的10个数据,进行一下核密度计算看看效果如何:
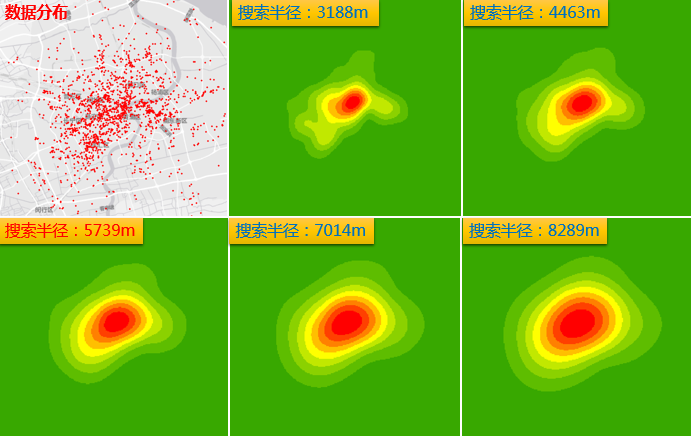
可以看见,对于全市范围的计算,聚类效果最显著的是搜索半径5739的区域。
现在我们再来看看不对全市的数据进行分析,仅仅对黄浦区的数据进行分析,计算之后,出现了两个峰值:
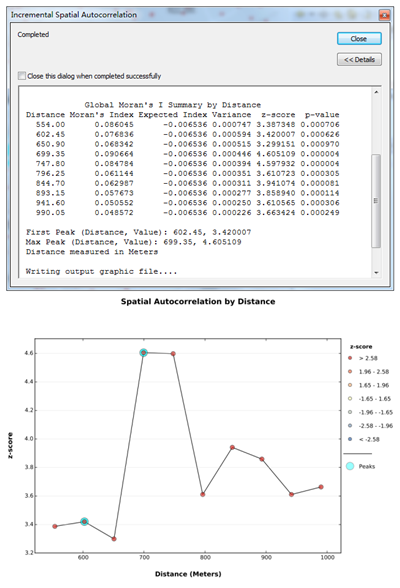
然后进行核密度计算:
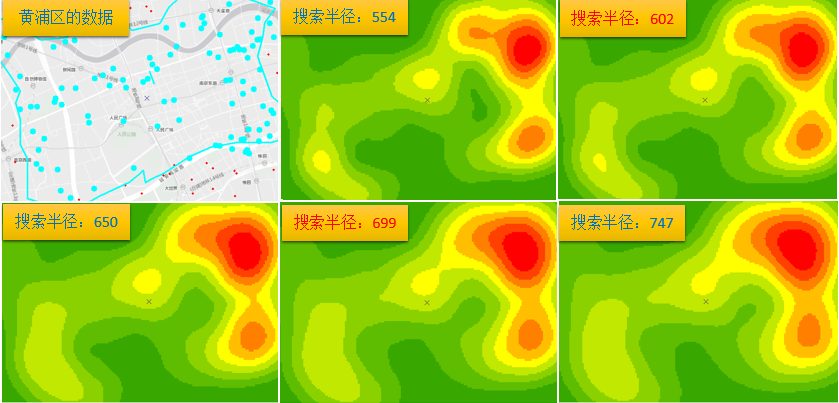
其中,602和699,是两个明显的峰值,也就是表示在这两个值,空间统计值是最显著的。
所谓的聚类,指的是让同类间差别最小,不同类之间差别最大,所以我们可以对比一下标成红色的的两个图,602和699,他们明显处于核密度曲线值变异的关键拐点上面,这也是我们使用这个工具,进行点数据分析之前进行探索时候的主要作用。

转载自:https://blog.csdn.net/allenlu2008/article/details/48350459