白话空间统计二十三：回归分析（二）

前缘再续，书接上一回……

要理解回归分析的这些特点（优点）以及特性，首先得了解一下回归分析的一些概念。

所谓“信息从来是一切的基础，世界上从不存在建立在空中楼阁上的智慧，搜集、处理信息本身就是一种智慧的体现”，只要有足够的信息，就能得到所需要的任何结论。君不见，在形容神的时候，把神称为“全知全能”……知还在能的前面……好吧，扯远了，回来继续我们的回归分析。

在分析任何事务之前，都要对信息进行数字化建模……而在目前信息化手段的帮助之下，不是数据太少，而是数据太多了……正如教材里面所谓的《XX编程大全》：——所谓的大全，不但要包括所有正确的内容，也包括了所有错误的内容……否则你怎么敢叫做大全呢。

所以在分析的时候我们用了各种各样的方法就是想把一些干扰项或者冗余项或者其他不重要的项神马的，都处理掉。这种计算在数据分析里面有一个特有的领域，或者是称之为“降维”，亦或者称之为“主成分”啥的。

最常用的简化数据方法，就是采用频数或者分组计算均值或者方差这样有统计代表性值表来进行，而回归分析也是一种简化数据的手段。其他的方式是采用特征值来标识一批数据，而回归分析是用一个自变量与因变量之间的简单函数来代表这种关系。通过这个函数，对自变量进行观察，然后对因变量的结果进行预测，并且使预测的结果尽可能的接近因变量的真实观察值。

对于预测这种提法，有一个不可回避的问题，就是实际观察值和预测出来的结果，肯定是偏差的（啥？你说要无偏差百分百正确？那我还写博客干嘛……老夫直接买彩票去好了……当然，要摆谱哲学，摇头晃脑的说“差之毫厘，失之千里”一类的话，那老夫就只能搬出码农界的一句大实话：先解决有没有，再解决好不好。）

而说到偏差，这里就不得不说回归分析的一个最重要的特征了，就是它把观测值分解成了两个部分：结构部分和随机部分。如下图所示：

结构项表示的是因变量与自变量之间的结构关系，那么随机项又是啥呢？如下：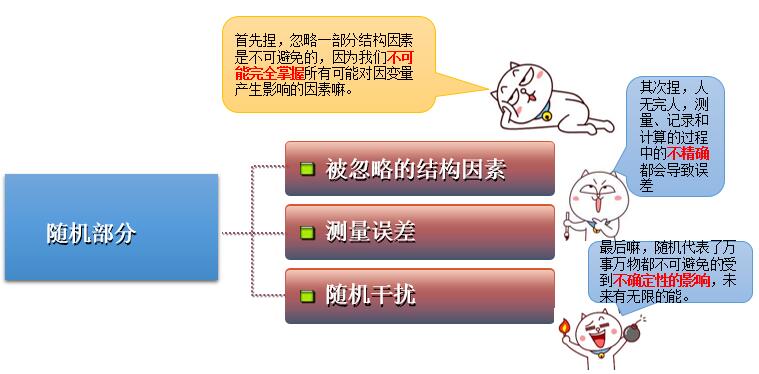

那么如何理解回归模型的意义呢？学术上针对回归模型提出了三种视角，也是定量分析的三种不同视角。

第一种方式 认为，回归模型是用来描述因果性关系的，这也是最接近古典计量经济学的视角。这种观点的把结构部分称之为“机制项”，即研究者想通过一个确定一个模型来发现这些数据事件产生的机制——找到因果关系。而随机部分，认为是对这种因果关系的一种干扰。如下图所示：

这种观点代表了回归模型的一个最经典的应用。所以在很长的一个时间段内，被奉为圭臬，到今天为止，大部分人也都认为回归就是因果。

但是随着研究的深入，更多的研究者认为决定性、真实无偏的模型是不存在的，好的模型只是相对其他模型而已更有效、更有意义或者更接近真实的情况……

第二种观点认为，回归模型是是用来进行预测的。这种视角更多的用于工程学领域。因为它通常是通过已知的一组自变量和因变量之间的关系后，用新的自变量来预测对应的因变量。比如，我们知道某种物体的强度是在生产的过程中与温度有密切关系，那么我们只需要系统的改变温度后就可以得到不同温度下该物体的强度样本。这样测量出足够多的数据之后，只需要建立一个模型，就可以找到得到各个所需强度的生产温度。

这种方法现在也被社会学家们进行了扩展和应用，来预测人类的行为。这一方法最大的特点是：只用经验规律来进行预测，对因果关系的机制不感兴趣。

第三种观点认为，回归分析就是用来认识和描述数据的，即不是“一锤定音”的因果律武器，也不是“未卜先知”的大预言术……它就是利用模型，来概括数据的基本特征。这种描述性的观点，也是当今各个定量分析学科的主流观点。

这种观点最主要的特点就是所谓的”奥卡姆剃刀原则”，即简约原则，简单来说，就是如果有一堆的模型，对观察项的解释都是差不多，那么除非找到其他证据来支持某一个模型，否则我们选最简单的。（虾神语录：简单粗暴才是王道）。

这种方法粗看起来，和因果观点差不多……都是确定最“合适”的模型嘛，但是二者有个本质的不同，因果观点认为：一定要确定一个“真实”的模型，而描述性观点认为，这个模型只要符合观察到的现实就行，至于是否“真实”，我就无所谓了。

其实，对于强迫症患者来说有一个福音——三种视角并不是相互排斥的，具体使用哪种，是根据我们的研究和目的来选定的，又是一个仁者见仁，智者见智，凶者见刀光剑影的过程……

不过一般来说，学术界目前更倾向第三种观点，也就是描述性观点，也是目前数据分析和数据挖掘界的一个共识：数据体现的是客观情况，和因果以及未来没有关系（无因有果和黑天鹅）。统计模型的主要目标在于用最简单的结构和尽可能少的参数来概括大量数据所包含的主要信息。

OK，到这里，回归分析的来历和解释就说到这里了，从下一章开始，通过数据和示例来继续聊回归分析。

转载自：https://blog.csdn.net/allenlu2008/article/details/55001288