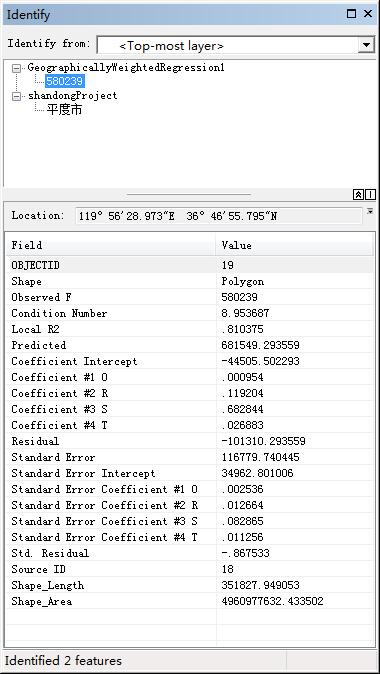
白话空间统计十八：相关性分析

其实这一章开始想放到了番外篇里面。因为相关性分析是经典统计学里面最基础也是最重要的分析方法之一。题目还是取了个白话空间统计，所以总是有点怪怪的。

不过空间统计要是完全脱离经典统计学去谈，那就真是坠入魔道了……计量革命最主要的成果之一，就是促成了经典统计分析方法在地理学研究中的应用。直到今天，经典统计学还是计量地理学中最常用的手段。可以说，空间统计学仍然是在经典统计学理论上建立和发展起来的。

在讲相关性分析之前，还是先要检讨一下，前面说了那么多空间相关性，而啥叫相关性分析，今天才写……就像我上面说的，坠入魔道了，把空间统计和经典统计分开在谈，确实是不应该的。以后凡是有这类的内容，我就不解释到底谁是严格的“空间统计学”或者是严格的“经典统计学”里面的内容了，正如下面的这句话：（图片内容来自《那年那兔那些事儿》版权归作者麻蛇，此次仅为引用）

那么什么叫做相关性分析呢？相关性分析的任务，主要是建议两个东西之间相互关系的紧密程度，如下图所示：

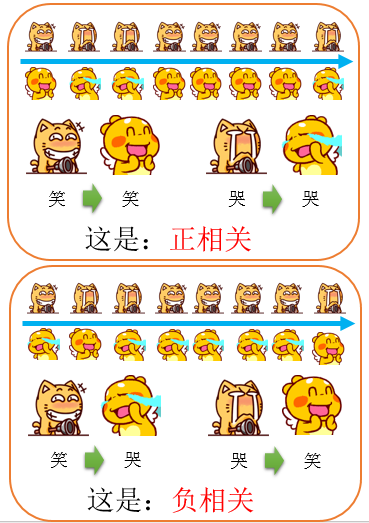
通过数学公式，可以计算出这个相关系数，相关系数的值一般都在【–1,1】之间，情况如下：

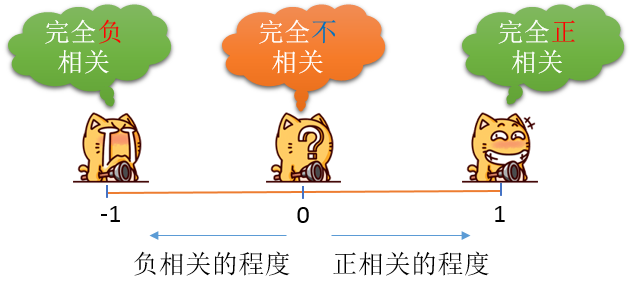
关于计算相关系数的公式，大家自己百度一下就行，以免有数学恐惧症的同学抓狂……

我们现在用最强大R语言，来对一下数据进行一下相关系数计算：

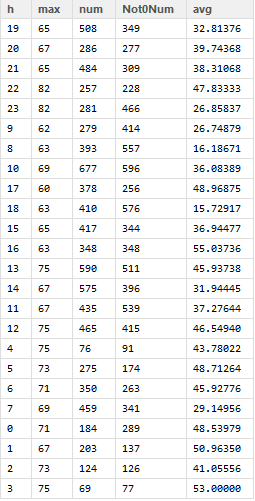
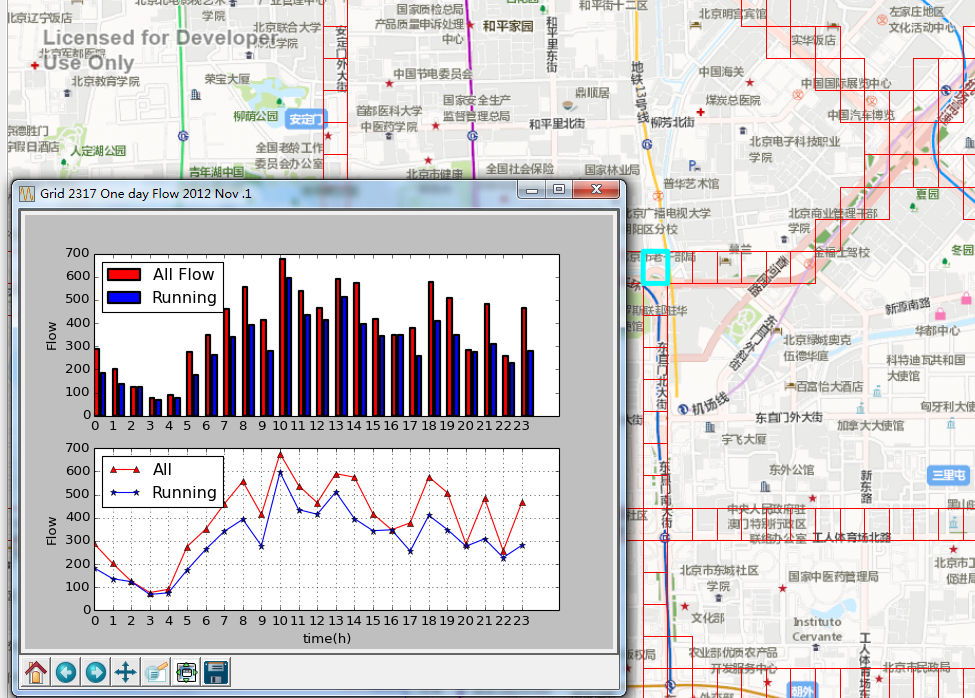
上面这个表，一下位置（格网编号2317）的当天24小时的出租车车流量与车速统计数据，如下：

上面有5个数据，我们依次用这五个数据，来计算一下相关性，相关性矩阵计算如下（因为是无向图，所以就不填入了重复的数据了）：

从上面的五个变量计算出来的相关性，可以看见，相关性最高的是总体车流量数与运行中的车辆数，而且是正相关，说明了如果这个格子里面的总体车辆数非常多的话，那么在运行中的出租车数量也相应增多。

第二高的是运行中的车辆数与整个格网中的平均时速，但是是负相关，也就说明了，如果运行中的车多，那么时速就会相应的降低。

当要素之间的相关系数计算出来之后，还需要对求出来的数据进行一下检验。为什么要检验呢，因为我们的相关系数是通过这些数据样本值计算出来的，样本数量的多少或者取值方式的不同，也会导致我们算出来的相关系数不同，一般来说，检验相关系数，都是通过相关系数检验表来计算的，如下：

上面这个就是相关系数检验表，一般大于这个表里面表示的值，我们就认为是相关性显著了，这个表在网上有下载，大家可以百度一下就搜索到了。

如何读取这个表呢，我们逐个来解释：

首先看自由度，自由度就是指你受约束的程度，我们都知道，受约束的情况，是随着条件越多，自由就越少，这里的自由度也是一样的，自由度数值越大，表示约束越多。

自由度的计算，一般是n-m-1，n表示你的样本数量，我们这里的样本数量是24个，m是因子数（m元回归），我们这里用一个值对比一个值，所以就是一元回归，所以我们的自由度
= 24 -1-1 = 22 。

上面那个0.1，0.05和0.01就是置信度，关于置信度的问题，请查看前面的“白话空间统计十三：零假设”，懒得查看的，看下面图片复习一下：

然后，我们用这个表里面的显著性，来对比一下我们的相似性矩阵，如下：

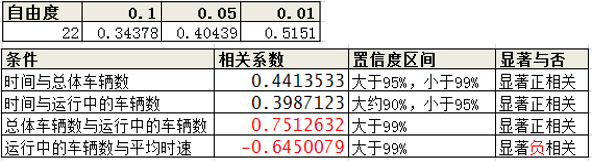
从以上表可以看出，只有4个条件有显著相关性，而如果我们将置信度区间设为95%的，就剩下三个了。

最后题外话：最后两个条件，也就是总体车辆与运行车辆正相关，运行车辆与平均时速负相关，是在没计算之前，就基本上猜到了，这就是常识嘛。但是在东直门这个交通枢纽上，时间与总体的车流量居然95%的置信度区间内显示出了显著正相关，确实我没有想到的。

当然，如果换一个区域计算，可能又有不同了，以后有机会，虾神会对不同时间不同研究区域的数据，都作一个相关分析，看看北京市交通到底会有一些什么好玩的表现出现，当然，大家有兴趣的，也可以做一下。