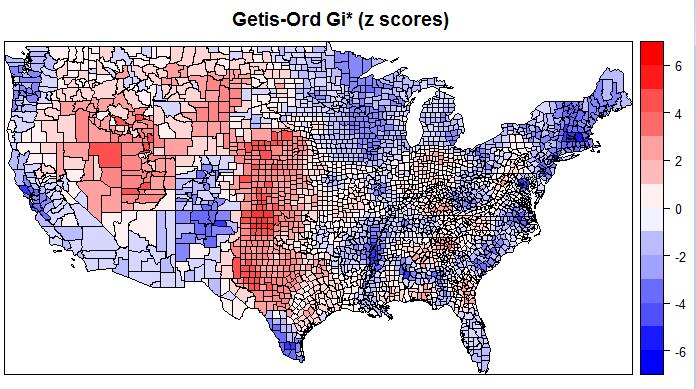
白话空间统计二十三：回归分析（五）

白话空间统计二十三：回归分析（五）回归应用

当然，在说这个之前，先回答大家关心的几个问题。关于回归分析写了四章了，不知道大家是不是和我一样有这样一个问题：这个东东我就看见了一堆概念，这个东西到底是干嘛的……而且：

please！！

好吧，今天就用大白话来说说，回归在实际的工程应用中到底是来干嘛。

比如，我们在分析的时候，拿到了这样一份数据：

现在咋办？当然，有同学说，介还不容易么？缺了我在分析的时候，直接remove掉这一条就OK了！嗯，现在我们来看看结果，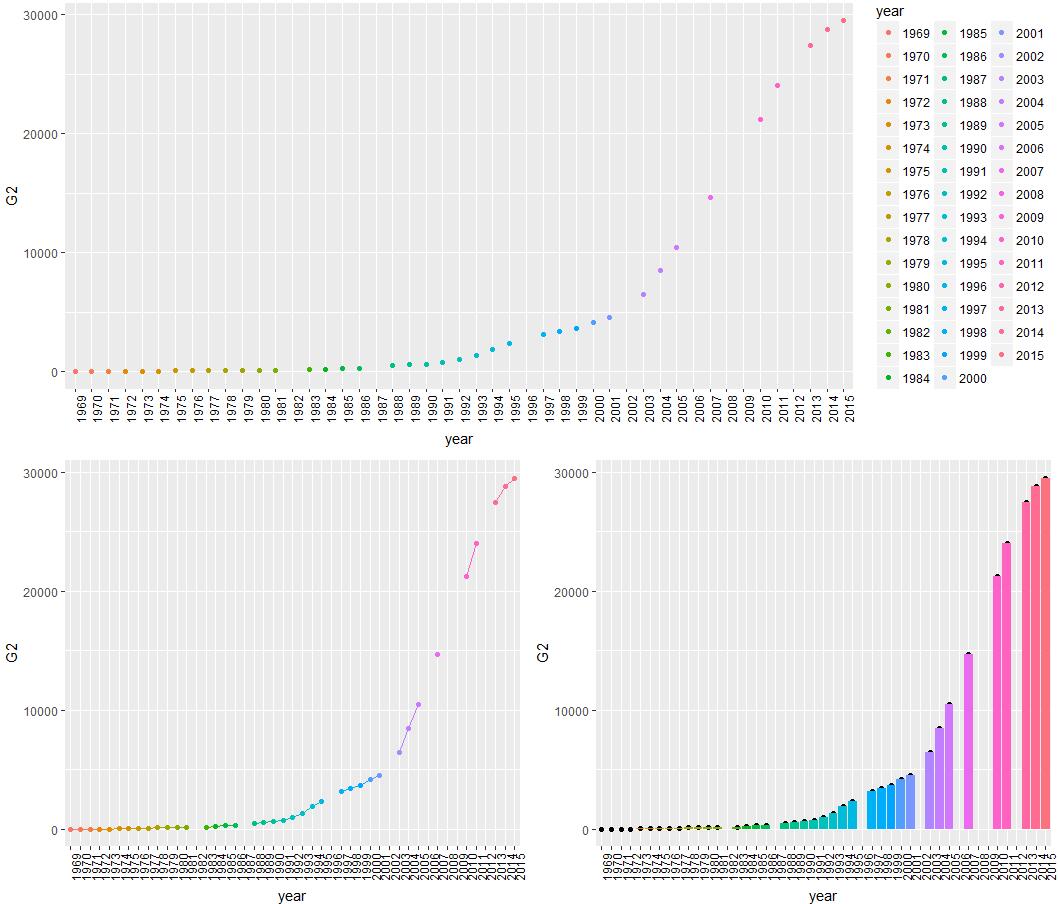

好吧，如果说点状数据还勉勉强强能够接受以外，那断断续续的折线图和坑坑洼洼的柱状图算神马？

然后，遇上这样的情况：

数据的缺失，在实际的工作中，是无法避免的事情，当然，在学术界，“缺失”和“不完整”是两个概念，我们这里用的“缺失”，指的是“实际存在，但是没有被记录”来表示。（具体关于缺失数据的概念，以后有机会再讨论）

而处理缺失数据最简单也是最经典的方法称之为补插，也就是采用预测的方法来对缺失数据进行填充，填充的方法最常用，也最容易理解的就是均值补插：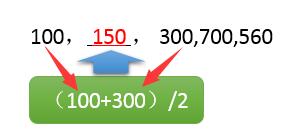

当然， 这种方法仅限于数值是定距型的情况（或是线性增长）嗯……我们上面的GDP值，就是这种类型，看样子能用，那么我们来试试：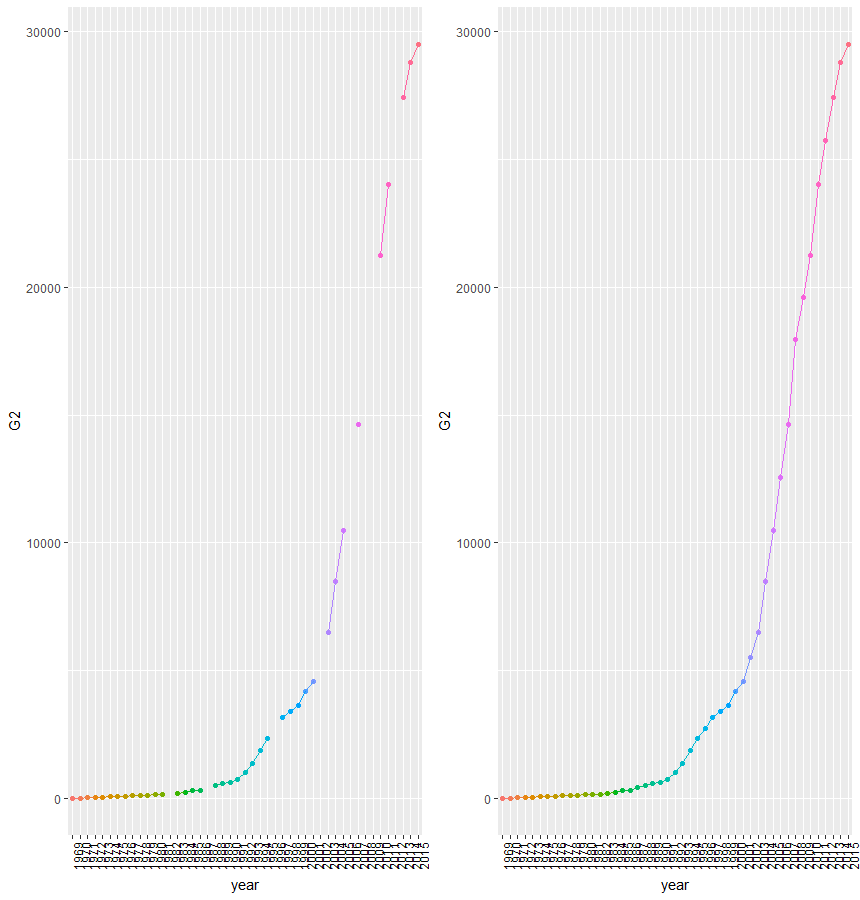

看看具体数值，（第三列newG2)看起来，还挺像那么回事的。第四列是实际的数据，那么实际上我们来看看，补全的数据与实际数据的一些统计值

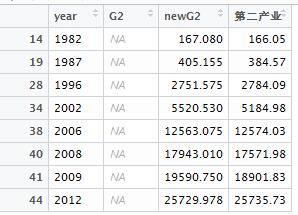
最大误差超过688……

那么有没有一个更好的办法来处理缺失值呢？当当当当（Intel广告铃），回归分析闪亮登场了。
当我用G1（第一产业）和G2进行一元回归的时候，结果如下：

通过统计信息，做出回归方程：
G2 = 6.0915*G1 – 1435.4413

现在通过这个直线方程，再来计算一次G2的缺失值：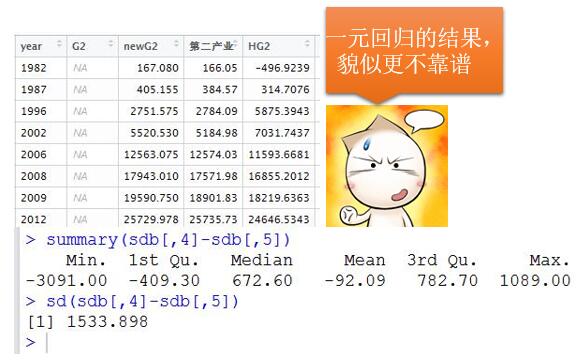

来试试二元回归？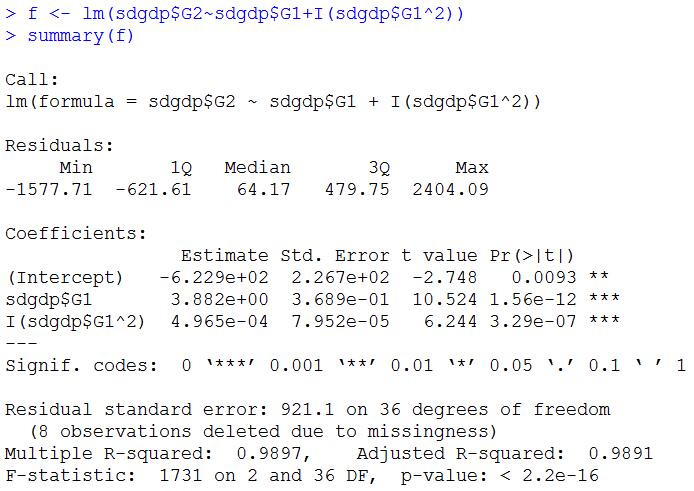

曲线方程如下：
0.0004965 * x*x + 3.882 * x – 0.06

结果如下：

为什么会这样呢？我们来具体看看：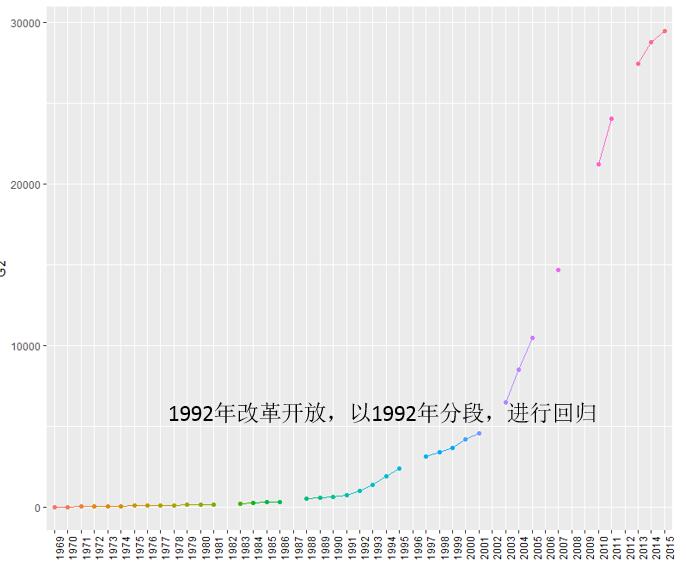

以92年分段，进行回归，得出如下结果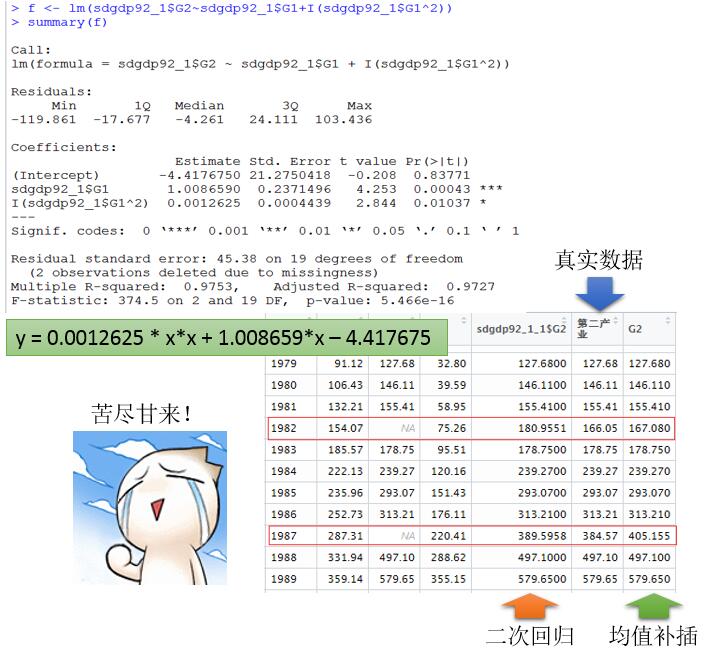

当然，这个回归方程的拟合程度还是不够，但是可以看出来，如果用回归来对缺失值进行出来的话，如果你方程足够优化，那么得出来的结果肯定要更好……

另外，还有个更重要的因素：均值补插，只支持定距型数据……如果是离散数据，均值补插法就只能看着呵呵了。

用于缺失值处理，是回归分析最主要也是最简单的应用之一，那么从下一章开始，进入地理加权回归阶段。如果回归分析还需要些的话，作为回归分析的番外篇进行加入。

（待续未完）

转载自：https://blog.csdn.net/allenlu2008/article/details/58072784