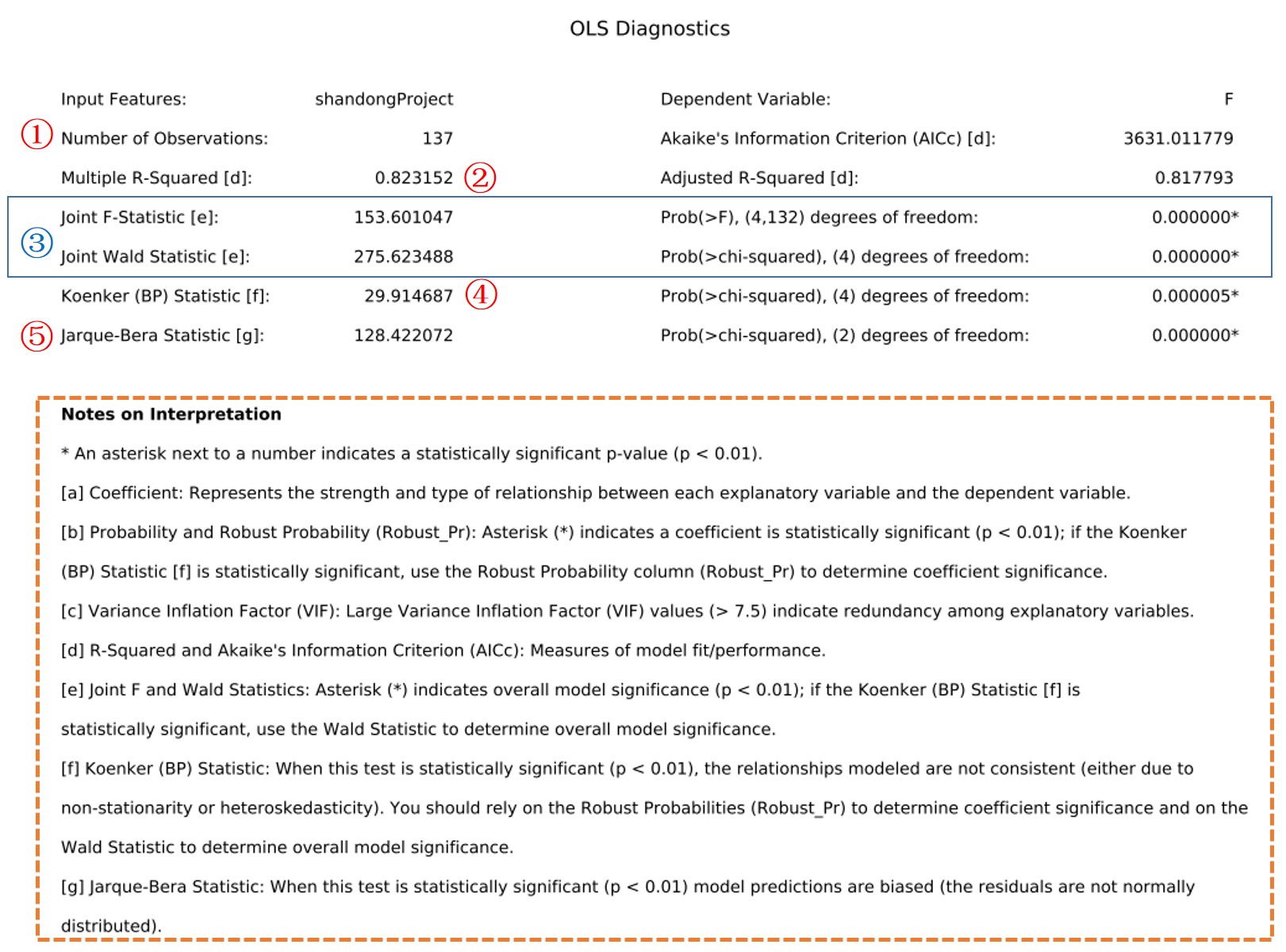
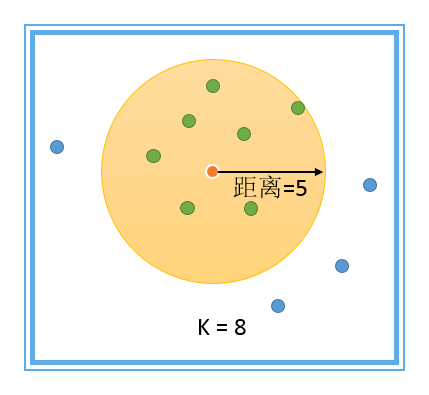
说在前面的话:前面花了好多章来讲各种数据分析的方法和样例,突然发现我原来设想的主线乱了。
我的设想是对空间统计进行科普型的描写叙述,结果写到后面,特别是这几章(准确说是从填中位数中心的算法坑開始),幸好有吴道长果断提醒,说我偏离方向了,我才豁然省悟。再次友情感谢吴道长(PS:吴道长是GIS圈子里面古玩玩的最好的,古玩界里面。GIS技术最好的综合性人才)。所以从今天開始。我继续把空间统计里面那些绕口的理论变成大白话写给大家。
好,继续今天的内容。事实上零如果这个内容在讲P值和Z得分的时候,已经专门用一章来讲述过了,可是好几次都遇上有人问我,而后又表示前面那一章文字描写叙述太多,没有看懂云云……所以我准备再花一章的内容,用图的方式来讲一讲。
事实上要说到零如果,最早也还是由罗纳德·艾尔默·费希尔(Ronald Aylmer Fisher 1890~1962)爵士在他的《试验设计》一书中提出的,就是前两天说线性平均方向那个费希尔爵士,要说统计算法,以后他老人家会反复反复再反复的出如今我们的文章中。由于作为“现代统计学之父”的费希尔爵士,号称是“以一己之力独立创建了现代统计学的天才”(丹麦统计学家,统计学史的作者安德斯·哈尔德语)。
再贴一张这位老帅哥的相片:

零如果在统计里面,是用来干嘛的呢?
简单的说。零如果最早是为了解决瞎猜的问题。
看以下这个样例:
如今进入经典统计学里面的标准演示样例——丢硬币:
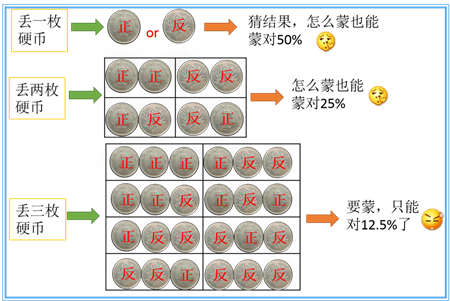
一个号称赌神的人,说他可以猜中丢出的硬币的正反。
如今来验证一下这个赌神是否名副事实上,然后我们来丢硬币。让这个赌神猜。那么假设仅仅丢三枚硬币的话。瞎猜也能蒙对12.5%。这可以说明赌神有猜中硬币的能力么?
为了证明(或者推翻)这个赌神确实有这个能力。所以就加大样本数量。比方:我们一次性丢出10枚硬币,例如以下:

10枚硬币,一共同拥有1024种组合,那么假设他是靠蒙得话。就仅仅有不到1%的可能猜对,而在这样的情况下,他还可以准确说对每一枚硬币的正反,那说明这个赌神的确有可能有猜中硬币正反的能力。
可是。是不是一定有呢?能不能消除瞎猜这个可能?继续加大硬币数量,比方扔出15枚硬币:

靠猜中的结果就变成了十万分之三了。可是无论你加多少硬币,都不可能把靠瞎蒙的机率减少到0。所以当这个机率下降到一定程度的时候,我们就说,已经拒绝了瞎猜的可能性,也就是拒绝了零如果。
费希尔爵士觉得,这个临界值就是5%,仅仅要是单纯靠瞎猜的成功率,超过了5%,那么就表示拒绝了零如果,而不须要达到1%甚至。
这个5%在各行各业中都在不断应用集成和发展。空间统计也是一样。
继续看样例。比方一个城市的犯罪事件,如果没有不论什么的附加条件,应该是这种:

也就是城市的每一个区域。他的犯罪率应该是同样的。
嗯当然也有可能是这样:

也就是说,在城市不论什么一个角落,都有可能发生案件。也有可能不发生。全然是随机的。
这与均匀分布不同的是,均匀分布是每一个角落都有且仅仅有一例(这是差点儿不可能的)。相对来说。随机发生的可能性就大非常多了,有可能这个区域一起都没有,也有可能连续发生好几起。
那么作为分析师,你首先要告诉我,拿到的这份数据是不是随机的,有没有随机的可能。
假设是随机的,就说明罪犯是无目的的犯罪,走哪逮哪,全然靠瞎蒙。
无目的的犯罪是最麻烦的,罪犯没有目的的瞎蒙。那么警察也仅仅能跟着瞎蒙……
为了不瞎蒙,就要先进行数据的探索和分析了。
首先。如果罪犯就是无目的的犯罪,如果可以推翻这个如果,自然就证明了罪犯是有目的的,这样才可以进一步进行分析。
这个如果罪犯是随机犯罪的过程,就是所谓的零如果。接下去计算这个零如果的可能性,也就是前面所过的p值和Z得分。如果符合真实的罪犯犯罪数据,与我们的如果有超过5%的重合可能,那么就真有可能这些罪犯的作案过程就真有可能是随机的。
步骤例如以下:

那么怎样判定是否拒绝了零如果呢?这份数据是否随机呢?请回头去看把话空间统计第四章:P值和Z得分。
最后,总结一句话:我们做的全部计算,最后的目的就是为了推翻零如果,零如果的存在,就是为了让我们去拒绝的。
 (看到这里。想到老夫就像零如果……被无数女生拒绝……遂有感而发)。
(看到这里。想到老夫就像零如果……被无数女生拒绝……遂有感而发)。