白话空间统计二十三：回归分析（四）

白话空间统计二十三：回归分析（四）

今天把回归最后几个概念介绍一下，后面就不再说了……开始写回归的时候，我发现我掉入了一个巨大的坑里面。就说回归分析这种东东，汗牛充栋啊，在任何大学里面，妥妥一个学期的课程，想用几篇文章写清楚，那几乎是不可能的，所以虾神准备过段从这个坑里面抽身（老衲法号从心——合起来就是“怂”），最后用几节讲讲概念，就进入我最擅长的软件或者代码部分。。。。

首先说说，回归线是怎么做出来的……嗯，先是一元回归，也就是最简单粗暴的直线。

作为直线，在平面坐标系里面，有两个重要的参数，分别是截距和斜率，如下：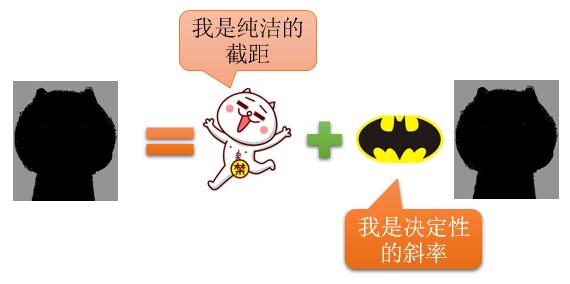

只要有这两个参数，就可以决定一条直线了，那么这两个东东是怎么求出来的呢？

如果最理想的状态，就是相关系数为1的时候，如下面的理想状态，截距为0，回归线完全穿过所有的点，也就表示观测值和预测值完全相匹配，这样来说，求回归线就没有任何难度了……但是实际上，应该是像实际情况这样的，观测值和预测值之间存在明显的误差，这样来说的话，如何来求呢？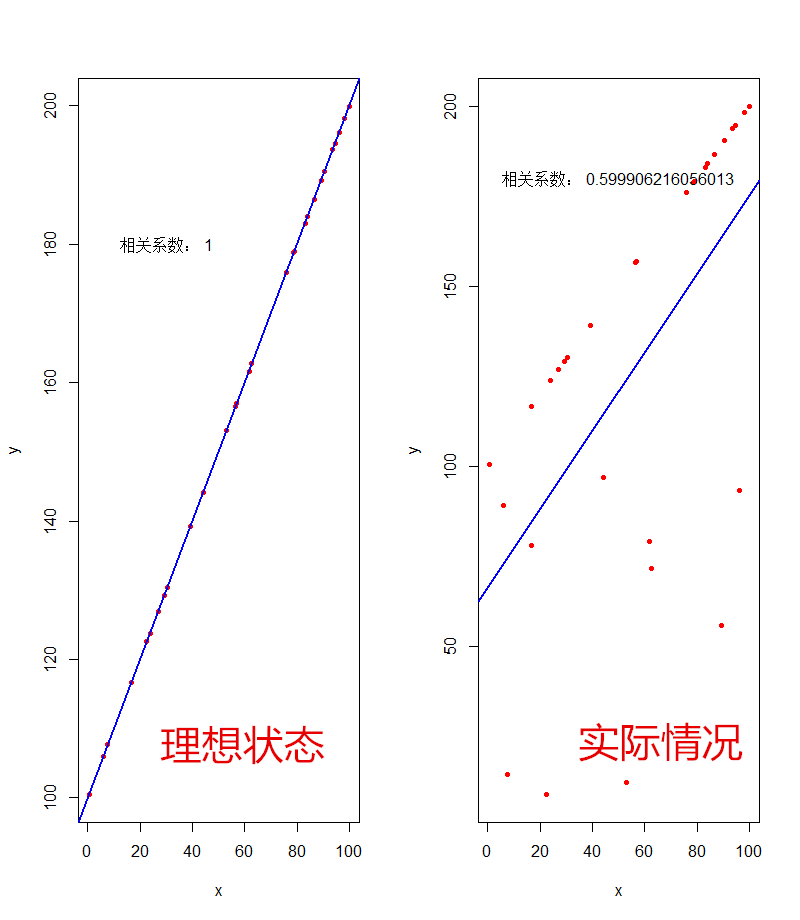

最常用的方法，称之为“最小二乘法”（ordinary least squares，简称：OLS）来求着两个参数，公式最后再贴，这里列出这种算法的一般思路即可。

OLS的基本思路，就是抽取一个样本点A1，找到离这个样本的最近的一个位置，称之为预测点B1，然后再抽一个点A2，把(A1,B1)放进来一起计算，找到一个点B2，并且使(A1-B1)^2 + (A2-B2)^2 最小的那个距离。以此类推……直到找到一条最合适的回归为止如下所示：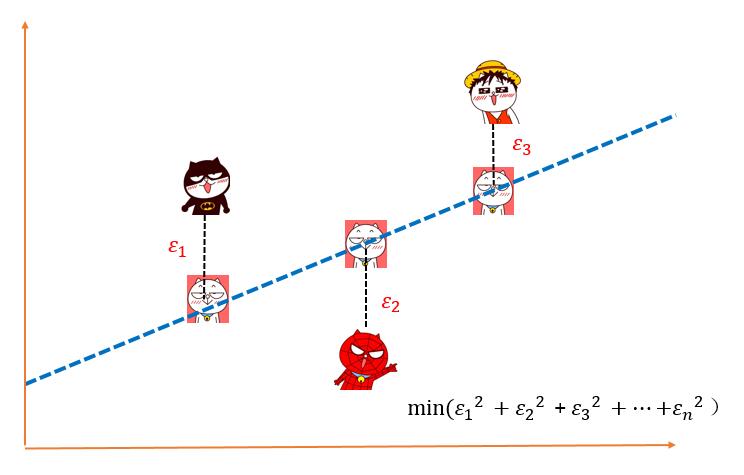

贴出计算公式来：（具体的公式推理过程，大家自己找资料）。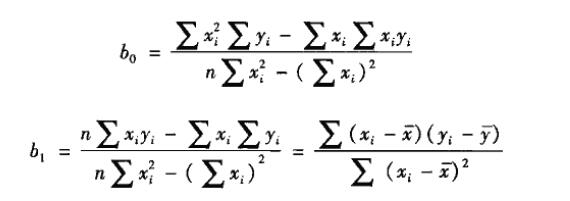

其中b0是截距，b1是斜率。

但是，根据数学原理来看，最小平方和未必是“最佳估计”的唯一值，如果仅仅要找到观测值和预测值之间距离最短的那个值，用距离绝对值之和的效果会更好。实际上也有用最小绝对距离计算的，这种方法得到的结果称之为“最小绝对偏差法（LAD）”估计值，它的优点是不太容易受到异常值对回归参数估计值的影响。

但是，最常用的方法还是OLS，因为这种方法的公式最简单，计算最方便（老话：简单粗暴是王道），而去计算得到的回归系数具有更好的统计性质，其线性、无偏性和有效性是最好的。

做出回归线来之后，如何判断这个回归的质量呢？也就是说，自变量X对因变量Y的解释程度有多高？回归分析里面，用拟合度（也有叫拟合优度:Goodness of Fit）这个参数来进行评判的。

啥叫拟合度呢？就是判断回归线与各个观测点的接近程度，一般来说，越接近就效果越好（特别是一元回归中，多元回归过度拟合也是一种病）。在一般回归里面，用判断系数来作为拟合度的判断指标。

判断系数的公式如下：

现在找两个极限数据，来进行一下评判，第一个是完全线性相关，第二个是完全随机：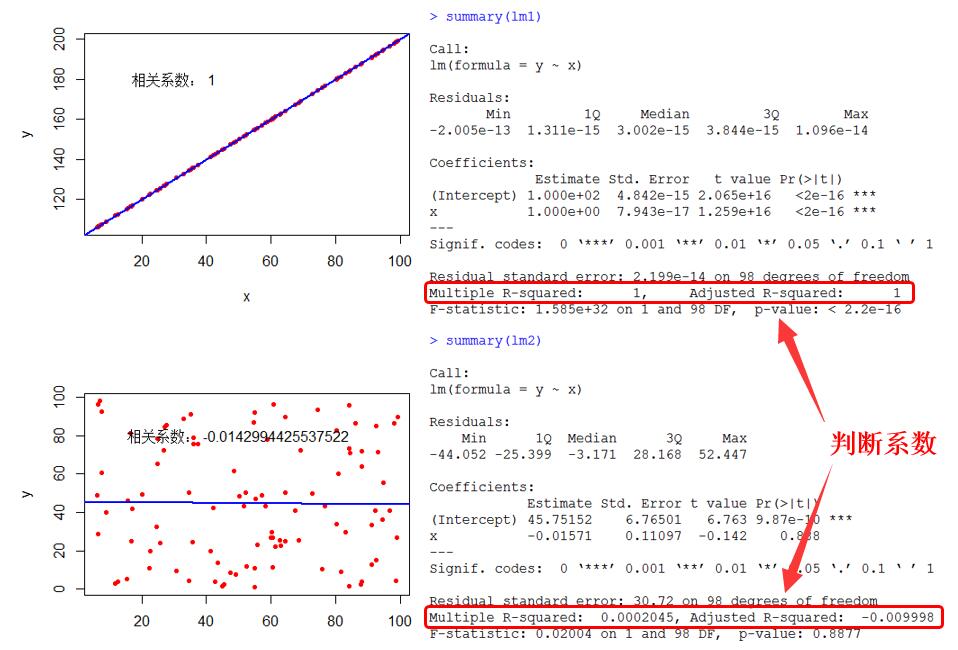

可以看见，完全拟合的话，判断系数为1，完全随机的话，判断系数无限接近0。

说到拟合，是不是拟合度越高就越好呢？在一定情况下，当然是越高越好，但是超过之后，中国有句老话，就叫过犹不及，比如下面这批数据：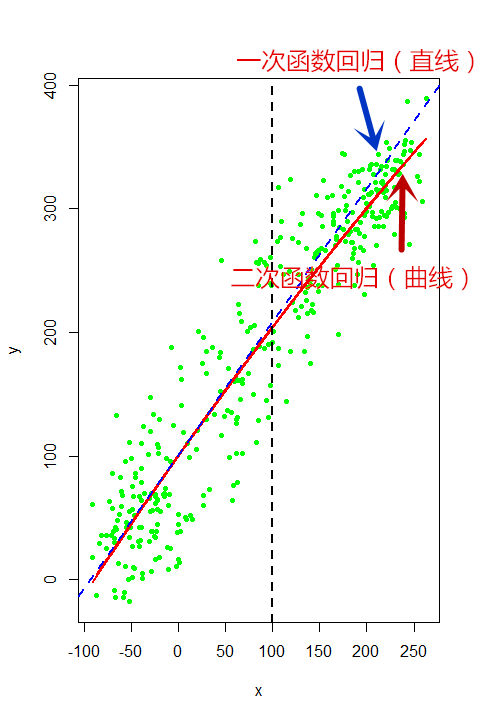

采用二次回归曲线的话，可以看见，当x超过100，Y超过200的时候，x与y之间变化会逐渐减少（逐渐进入平稳），这样可以看出比直接使用直线要好，结果如下：一次回归的判断系数为0.8813，二次回归的判断系数为0.8821

但是，如果我们追求更高的判断系数的话，也就是回归线穿过所有的点：就变成了一下这种情况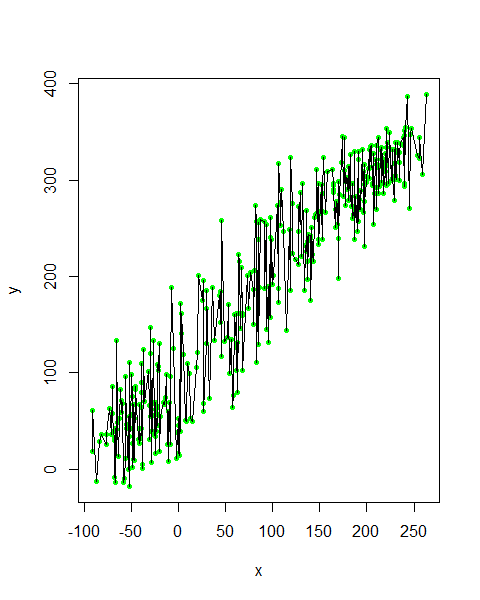

这样一来，回归线就已经没有任何意义了……

用常用的一句话说，啥叫过拟合呢？过拟合就是“看书看多，学傻了……”，下面通过一个小笑话，来解释一下过拟合：

待续未完

转载自：https://blog.csdn.net/allenlu2008/article/details/56016124